Question

【题目】如图，抛物线y=﹣ 与x轴交于点A，点B，与y轴交于点C，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．

（1）求点A、点B、点C的坐标；
（2）求直线BD的解析式；
（3）当点P在线段OB上运动时，直线l交BD于点M，试探究m为何值时，四边形CQMD是平行四边形；
（4）在点P的运动过程中，是否存在点Q，使△BDQ是以BD为直角边的直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：∵令x=0得；y=2，

∴C（0，2）．

∵令y=0得：﹣ =0，

解得：x1=﹣1，x2=4．

∴A（﹣1，0），B（4，0）．

（2）

解：∵点C与点D关于x轴对称，

∴D（0，﹣2）．

设直线BD的解析式为y=kx﹣2．

∵将（4，0）代入得：4k﹣2=0，

∴k= ．

∴直线BD的解析式为y= x﹣2．

（3）

解：如图1所示：

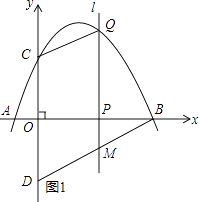
∵QM∥DC，

∴当QM=CD时，四边形CQMD是平行四边形．

设点Q的坐标为（m，﹣ m2+ m+2），

则M（m， m﹣2），

∴﹣ m2+ m+2﹣（ m﹣2）=4，

解得：m=2，m=0（不合题意，舍去），

∴当m=2时，四边形CQMD是平行四边形；

（4）

解：存在，设点Q的坐标为（m，﹣ m2+ m+2），

∵△BDQ是以BD为直角边的直角三角形，

∴①当∠QBD=90°时，

由勾股定理得：BQ2+BD2=DQ2，

即（m﹣4）2+（﹣ m2+ m+2）2+20=m2+（﹣ m2+ m+2+2）2，

解得：m=3，m=4（不合题意，舍去），

∴Q（3，2）；

②当∠QDB=90°时，

由勾股定理得：BQ2=BD2+DQ2，

即（m﹣4）2+（﹣ m2+ m+2）2=20+m2+（﹣ m2+ m+2+2）2，

解得：m=8，m=﹣1，

∴Q（8，﹣18），（﹣1，0），

综上所述：点Q的坐标为（3，2），（8，﹣18），（﹣1，0）．

【解析】本题考查了二次函数综合题，涉及的知识点有：坐标轴上点的特点，待定系数法求直线的解析式，平行四边形的判定和性质，勾股定理，方程思想和分类思想的运用，综合性较强，有一定的难度．（1）根据函数解析式列方程即可得到结论；（2）由点C与点D关于x轴对称，得到D（0，﹣2），解方程即可得到结论；（3）如图1所示：根据平行四边形的性质得到QM=CD，设点Q的坐标为（m，﹣ m2+ m+2），则M（m， m﹣2），列方程即可得到结论；（4）设点Q的坐标为（m，﹣ m2+ m+2），分两种情况：①当∠QBD=90°时，根据勾股定理列方程求得m=3，m=4（不合题意，舍去），②当∠QDB=90°时，根据勾股定理列方程求得m=8，m=﹣1，于是得到结论．
【考点精析】关于本题考查的确定一次函数的表达式和勾股定理的概念，需要了解确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案．