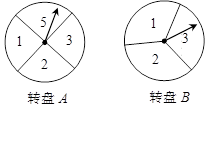Question

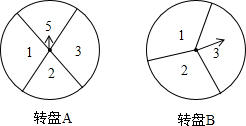
分别把带有指针的圆形转盘A、B分成4等份、3等份的扇形区域，并在每一个小区域内标上数字（如图所示）．欢欢、乐乐两个人玩转盘游戏，游戏规则是：同时转动两个转盘，当转盘停止时，若指针所指两区域的数字之积为奇数，则欢欢胜；若指针所指两区域的数字之积为偶数，则乐乐胜；若有指针落在分割线上，则无效，需重新转动转盘．
（1）试用列表或画树状图的方法，求欢欢获胜的概率；
（2）请问这个游戏规则对欢欢、乐乐双方公平吗？试说明理由．

Answer 1

分析：（1）列举出所有情况，看指针所指两区域的数字之积为奇数的情况占总情况的多少即可求得欢欢胜的概率；
（2）由（1）进而求得乐乐胜的概率，比较两个概率即可．

解答：解：

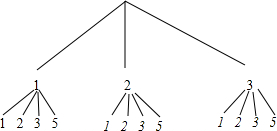
（1）共有12种情况，积为奇数的情况有6种情况，所以欢欢胜的概率是

6

12

=

1

2

；
（2）由（1）得乐乐胜的概率为1-

1

2

=

1

2

，两人获胜的概率相同，所以游戏公平．

点评：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=

m

n

，注意本题是放回实验．解决本题的关键是得到相应的概率，概率相等就公平，否则就不公平．