题目内容
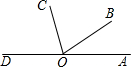
 如图,点O是直线AD上一点,射线OC、OE分别是∠AOB,∠BOD的平分线,若∠AOC=28°,则∠COD=
如图,点O是直线AD上一点,射线OC、OE分别是∠AOB,∠BOD的平分线,若∠AOC=28°,则∠COD=分析:先根据∠AOC+∠COD=180°求出∠COD的度数,再根据角平分线的性质求出∠AOB的度数,由平角的性质可求出∠DOB的度数,OE是∠BOD的平分线即可求出∠BOE的度数.
解答:解:∵∠AOC+∠COD=180°,∠AOC=28°,
∴∠COD=152°;
∵OC是∠AOB的平分线,∠AOC=28°,
∴∠AOB=2∠AOC=2×28°=56°,
∴∠BOD=180°-∠AOB=180°-56°=124°,
∵OE是∠BOD的平分线,
∴∠BOE=
∠BOD=
×124°=62°.
故答案为:152°、62°.
∴∠COD=152°;
∵OC是∠AOB的平分线,∠AOC=28°,
∴∠AOB=2∠AOC=2×28°=56°,
∴∠BOD=180°-∠AOB=180°-56°=124°,
∵OE是∠BOD的平分线,
∴∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:152°、62°.
点评:本题考查的是角平分线的定义,即从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 7、如图,点O是直线AD上的点,∠AOB,∠BOC,∠COD三个角从小到大依次相差25°,则这三个角的度数是
7、如图,点O是直线AD上的点,∠AOB,∠BOC,∠COD三个角从小到大依次相差25°,则这三个角的度数是