题目内容
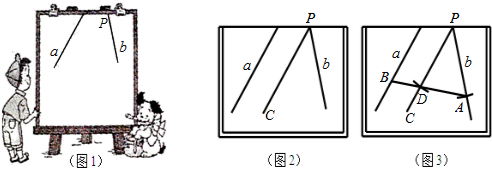
提出问题:如图,有一块分布均匀的等腰三角形蛋糕(AB=BC,且BC≠AC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
背景介绍:这条分割直线即平分了三角形的面积,又平分了三角形的周长,我们称这条线为三角形的“等分积周线”.尝试解决:
(1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.

(2)小华觉得小明的方法很好,所以自己模仿着在图1中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗如能成功,说出确定的方法;如不能成功,请说明理由.
(3)通过上面的实践,你一定有了更深刻的认识.请你解决下面的问题:若AB=BC=5cm,AC=6cm,请你找出△ABC的所有“等分积周线”,并简要的说明确定的方法.
背景介绍:这条分割直线即平分了三角形的面积,又平分了三角形的周长,我们称这条线为三角形的“等分积周线”.尝试解决:
(1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.

(2)小华觉得小明的方法很好,所以自己模仿着在图1中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗如能成功,说出确定的方法;如不能成功,请说明理由.
(3)通过上面的实践,你一定有了更深刻的认识.请你解决下面的问题:若AB=BC=5cm,AC=6cm,请你找出△ABC的所有“等分积周线”,并简要的说明确定的方法.
(1)作线段AC的中垂线BD即可.(2分)
(2)小华不会成功.
若直线CD平分△ABC的面积
那么S△ADC=S△DBC
∴
AD•CE=
BD•CE
∴BD=AD(4)
∵AC≠BC
∴AD+AC≠BD+BC
∴小华不会成功.

(3)①若直线经过顶点,则AC边上的中垂线即为所求.
②若直线不过顶点,可分以下三种情况:
(a)直线与BC、AC分别交于E、F,如图所示
过点E作EH⊥AC于点H,过点B作BG⊥AC于点G
易求,BG=4,AG=CG=3
设CF=x,则CE=8-x
由△CEH∽△CBG,可得EH=
(8-x)
根据面积相等,可得
•x•
(8-x)=6,
∴x=3(舍去,即为①)或x=5
∴CF=5,CE=3,直线EF即为所求直线.
(b)直线与AB、AC分别交于M、N,如图所示,
由(a)可得,AM=3,AN=5,直线MN即为所求直线.
(仿照上面给分)
(c)直线与AB、BC分别交于P、Q,如图所示
过点A作AY⊥BC于点Y,过点P作PX⊥BC于点X
由面积法可得,AY=
 ,
,
设BP=x,则BQ=8-x,
由相似,可得PX=
x,
根据面积相等,可得
•
x•(8-x)=6(11分),
∴x=
>5(舍去)或x=
.
而当BP=
时,BQ=
>5,舍去.
∴此种情况不存在.(12分)
综上所述,符合条件的直线共有三条.
(注:若直接按与两边相交的情况分类,也相应给分)
(2)小华不会成功.
若直线CD平分△ABC的面积

那么S△ADC=S△DBC
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴BD=AD(4)
∵AC≠BC
∴AD+AC≠BD+BC
∴小华不会成功.

(3)①若直线经过顶点,则AC边上的中垂线即为所求.
②若直线不过顶点,可分以下三种情况:
(a)直线与BC、AC分别交于E、F,如图所示
过点E作EH⊥AC于点H,过点B作BG⊥AC于点G
易求,BG=4,AG=CG=3
设CF=x,则CE=8-x
由△CEH∽△CBG,可得EH=
| 4 |
| 5 |

根据面积相等,可得
| 1 |
| 2 |
| 4 |
| 5 |
∴x=3(舍去,即为①)或x=5
∴CF=5,CE=3,直线EF即为所求直线.
(b)直线与AB、AC分别交于M、N,如图所示,
由(a)可得,AM=3,AN=5,直线MN即为所求直线.
(仿照上面给分)
(c)直线与AB、BC分别交于P、Q,如图所示
过点A作AY⊥BC于点Y,过点P作PX⊥BC于点X
由面积法可得,AY=
| 24 |
| 5 |
 ,
,设BP=x,则BQ=8-x,
由相似,可得PX=
| 24 |
| 25 |
根据面积相等,可得
| 1 |
| 2 |
| 24 |
| 25 |
∴x=
8+
| ||
| 2 |
8-
| ||
| 2 |
而当BP=
8-
| ||
| 2 |
8+
| ||
| 2 |
∴此种情况不存在.(12分)
综上所述,符合条件的直线共有三条.
(注:若直接按与两边相交的情况分类,也相应给分)

练习册系列答案
相关题目
 的图形.(全部用上,互不重合且不留空隙),并把你的拼法依照图示按实际大小画在方格内(方格为1cm×1cm)
的图形.(全部用上,互不重合且不留空隙),并把你的拼法依照图示按实际大小画在方格内(方格为1cm×1cm)