题目内容
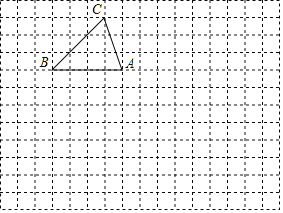
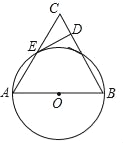
【题目】如图,以△ABC的边AB为直径作⊙O交AC于点E且AE=CE,过点E作DE⊥BC于点D.
(1)求证ED是⊙O的切线;
(2)若CD=1,sinC=![]() ,求AB的长.
,求AB的长.
【答案】(1)见解析;(2)5.
【解析】
(1)连接OE,只要证明OE⊥DE即可;
(2)连接BE,根据AB是直径,得到∠AEB=∠CEB =90°,利用∠CEB=∠CDE=90°,从而得到△DCE∽△CBE,利用对应边的比相等得到CB的值,然后在Rt△ABC中,AE=CE,∠AEB=∠CEB=90°,得出AB=BC,得出答案AB=5.
(1)连接OE.
∵AE=CE,AO=OB,
∴OE∥BC.
又∵DE⊥BC,
∴∠EDC=90°,
∴∠DEO=90°,
∴ED是⊙O的切线.
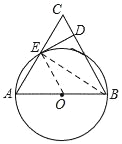
(2)连接BE.
在Rt△DCE中,CD=1,sinC=![]() ,
,
∴DE=2,CE=![]() .
.
∵AB是直径,
∴∠AEB=∠CEB=90°.
∵∠C=∠C,∠CEB=∠CDE=90°,
∴△DCE∽△CBE,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴CB=5.
∵AE=CE,∠AEB=∠CEB=90°,
∴AB=CB=5.

练习册系列答案
相关题目