题目内容
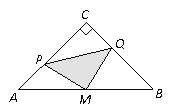
【题目】如图,在△ABC中,∠C=90°,AC=BC=4cm,M是AB的中点,点P、Q分别从A、C两点同时出发,以1cm/s的速度沿AC、CB方向均速运动,到点C、B时停止运动,设运动时间为![]() ,△PMQ的面积为S (cm2),则S (cm2)与
,△PMQ的面积为S (cm2),则S (cm2)与![]() 的函数关系可用图象表示为( )
的函数关系可用图象表示为( )
A.  B.
B. 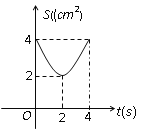 C.
C.  D.
D. 
【答案】B
【解析】当t=0时,点P与点A重合,点Q与点C重合,如图所示:
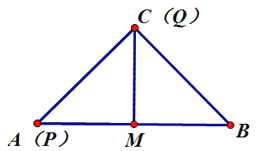
此时面积S△PMQ=![]() ;
;
当1<t≤2时,如图所示:

∵∠C=90°,AC=BC=4,
∴∠A=∠BCM=45°,MC=AM=![]() ,
,
又∵点P、Q分别从A、C两点同时出发,以1cm/s的速度沿AC、CB方向均速运动,
∴AP=CM=t
∴△APM≌△CQM(SAS)
∴S△PMQ=S△AMC- S△PCQ=4- ![]() =
=![]() ,
,
当t=2时,即点P、Q分别是AC、AB中点时,S△PMQ有最小值为2,
当t=4时,即点P与C重合,Q与B重合时,S△PMQ有最大值为4;
故选B。

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目