题目内容
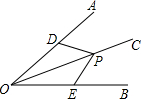如图，P是∠AOB的角平分线OC上的一点，点D、E分别在OA、OB上，且OD=OE，则判定△OPD≌△OPE的依据是
- A.A．S．A
- B.S．A．S
- C.A．A．S
- D.S．S．S
B
分析：根据题意，OC是∠AOB的角平分线，则∠AOC=∠BOC，又OD=OE，OP为公共边，即可判定出；
解答：∵OC是∠AOB的角平分线，
∴∠AOC=∠BOC，
在△OPD和△OPE中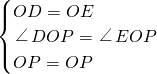
，
∴△OPD≌△OPE（SAS）．
故选B．
点评：本题主要考查了全等三角形的判定方法-SAS，两边及其夹角分别对应相等的两个三角形全等．
分析：根据题意，OC是∠AOB的角平分线，则∠AOC=∠BOC，又OD=OE，OP为公共边，即可判定出；
解答：∵OC是∠AOB的角平分线，
∴∠AOC=∠BOC，
在△OPD和△OPE中
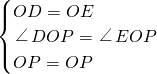，∴△OPD≌△OPE（SAS）．
故选B．
点评：本题主要考查了全等三角形的判定方法-SAS，两边及其夹角分别对应相等的两个三角形全等．
练习册系列答案
相关题目
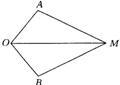25、如图，OM是∠AOB的平分线，MA⊥OA，交OA于A，MB⊥OB，交OB于B，如果∠AOB=120°，则∠AMO=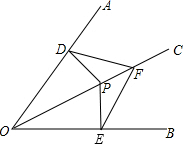
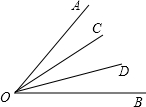如图，OC是∠AOB的平分线，OD是∠COB的平分线，∠AOD=60°，则∠AOB=
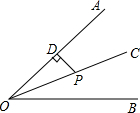如图，OC是∠AOB的平分线，PD⊥DA于点D，PD=2，则P点到OB的距离是（ ）
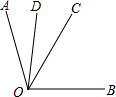如图，OC是∠AOB的平分线，OD平分∠AOC，且∠COD=25°，求∠AOB的度数．