Question

【题目】如图，已知△ABC中，∠B＝48°，∠C＝62°，点E、点F分别在边AB和边AC上，将把△AEF沿EF折叠得△DEF，点D正好落在边BC上（点D不与点B．点C重合）．

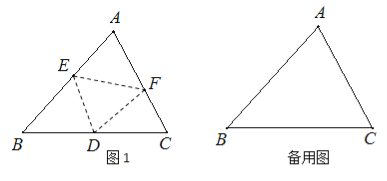
（1）如图1，若BD=BE，则△CDF是否为等腰三角形？请说明理由．

（2）△BDE、△CDF能否同时为等腰三角形？若能，请画出所有可能的图形，并直接指出△BDE、△CDF的三个内角度数；若不能，请说明理由．

Answer 1

【答案】（1）△CDF不是等腰三角形，理由见试题解析；（2）△BDE、△CDF能同时为等腰三角形，内角度数为：∠BDE＝∠B＝48°，∠BED＝84°，∠FDC＝∠C＝62°，∠DFC＝56°．

【解析】

试题分析：（1）利用三角形内角和算出∠A，等腰三角形性质算出∠BDE，再用折叠性质得到∠EDF=∠A，根据平角性质得到∠CDF，再算出∠DFC，进行判断即可；（2）若△BDE为等腰三角形，共有三种可能：

①BD=BE；由（1）可知，若BD=BE，则△CDF不是等腰三角形；

②BE=ED，可得：∠EDB=∠B=48°，又∠EDF=∠A=70°，得到∠FDC的度数；进行判断即可；

③BD=ED，同样求出∠BDE和∠CDF，∠DFC，然后进行判断．

试题解析：（1）△CDF不是等腰三角形；理由：

∵∠B＝48°，∠C＝62°，∴∠A＝180°-48°-62°=70°，

∵BD=BE，∴∠BDE＝(180°-48°)÷2=66°，

∵△AEF沿EF折叠得△DEF，∴∠EDF=∠A＝70°，

∴∠FDC＝180°-66°-70°=44°，∴∠DFC＝180°-44°-62°=74°，

∴△CDF不是等腰三角形．

（2）△BDE、△CDF能同时为等腰三角形．

∵△BED为等腰三角形，共有三种情况，BD=BE，BE=ED，BD=ED.

①若BD=BE；由（1）可知，若BD=BE，则△CDF不是等腰三角形；

②若BE=ED，可得：∠EDB=∠B=48°，又∵∠EDF=∠A=70°，∴∠FDC=180°－48°-70°=62°，∵∠C=62°，∴△DFC是等腰三角形，此时：∠BDE＝∠B＝48°，∠BED＝84°，∠FDC＝∠C＝62°，∠DFC＝56°；

③若BD=ED，则∠B=∠BED=48°，∴∠EDB=180°－48°－48°=84°，∴∠FDC=180°－∠EDF－∠BDE=180°－84°－70°=26°，∠DFC=180°－∠C－∠CDF=180°－62°－26°=92°，此时△DCF不是等腰三角形；

∴只有一种情况：∠BDE＝∠B＝48°，∠BED＝84°，∠FDC＝∠C＝62°，∠DFC＝56°．