题目内容

三角形内一点到各顶点的距离是该线段的

2

3

，则这点是三角形

．

分析：根据题意，画出图形，由中位线定理求得各线段之间的关系，再判断求解．

解答：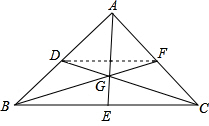

解：设AE、BF、CD分别是△ABC的中线，G为交点，连接DF
由中位线定理
DF∥BC，

DF

BC

=

1

2

∴△DFG∽△BCG
∴

DG

CG

=

FG

BG

=

1

2

即CG=2DG，BG=2FG
同理AG=2GD
∴三角形的三条中线交于一点，这点到顶点的距离是它到对边中点距离的2倍
∴三角形内一点到各顶点的距离是该线段的

2

3

∴这点是三角形三条中线的交点．

点评：三角形的三条中线交于一点，这一点称作三角形的重心．

练习册系列答案

创优考100分系列答案

高分中考系列答案

金牌教辅培优优选卷期末冲刺100分系列答案

中考专项突破系列答案

全能金卷小学毕业升学全程总复习系列答案

新课程同步导学练测八年级英语下册系列答案

精致课堂有效反馈系列答案

小考状元必备测试卷系列答案

全能小考王小升初名校备考密卷系列答案

中考5月冲关卷系列答案

相关题目

（2013•舟山）小明在做课本“目标与评定”中的一道题：如图1，直线a，b所成的角跑到画板外面去了，你有什么办法量出这两条直线所成的角的度数？

（1）①请帮小明在图2的画板内画出你的测量方案图（简要说明画法过程）；
②说出该画法依据的定理．
（2）小明在此基础上进行了更深入的探究，想到两个操作：
①在图3的画板内，在直线a与直线b上各取一点，使这两点与直线a、b的交点构成等腰三角形（其中交点为顶角的顶点），画出该等腰三角形在画板内的部分．
②在图3的画板内，作出“直线a、b所成的跑到画板外面去的角”的平分线（在画板内的部分），只要求作出图形，并保留作图痕迹．
请你帮小明完成上面两个操作过程．（必须要有方案图，所有的线不能画到画板外，只能画在画板内）

加试题（本小题满分20分，其中（1）、（2）、（3）题各3分，（4）题11分）
（1）一个正数的平方根为3-a和2a+3，则这个正数是

（2）若x²+2x+y²-6y+10=0，则x^y=

（3）已知a，b分别是6-

的整数部分和小数部分，则2a-b=

（4）阅读下面的问题，并解答问题：
1）如图1，等边△ABC内有一点P，若点P到顶点A，B，C的距离分别为3，4，5，求∠APB的度数是多少？（请在下列横线上填上合适的答案）
分析：由于PA，PB，PC不在同一个三角形中，为了解决本题我们可以将△ABP绕顶点A逆时针旋转到△ACP′处，此时可以利用旋转的特征等知识得到：
①∠APB=∠AP′C=∠AP′P+∠PP′C；
②AP=AP′，且∠PAP′=

度，所以△APP′为

三角形，则∠AP′P=

度；
③P′C=BP=4，P′P=AP=3，PC=5，所以△PP′C为

三角形，则∠PP′C=

度，从而得到∠APB=

度．
2）请你利用第1）题的解答方法，完成下面问题：
如图2，在△ABC中，∠CAB=90°，AB=AC，E、F为边BC上的点，且∠EAF=45°，试说明：EF²=BE²+FC²．

三角形内一点到各顶点的距离是该线段的 $数学公式$ ，则这点是三角形________．

三角形内一点到各顶点的距离是该线段的

，则这点是三角形．