题目内容
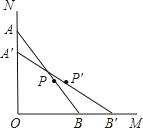
【题目】如图，一根木棒（AB）长为2a，斜靠在与地面（OM）垂直的墙壁（ON）上，与地面的倾斜角（∠ABO）为60°，当木棒A端沿N0向下滑动到A′，AA′=（
）a，B端沿直线OM向右滑动到B′，则木棒中点从P随之运动到P′所经过的路径长为_____．
【答案】
【解析】解：连接OP、OP′，如图．∵ON⊥OM，P为AB中点，∴OP=
AB=A′B′=OP′．∵AB=2a
∴OP=a，当A端下滑B端右滑时，AB的中点P到O的距离始终为定长a，∴P是随之运动所经过的路线是一段圆弧．∵∠ABO=60°，∴∠AOP=30°，OA=
a．∵AA′=（﹣
）a，OA′=OA﹣AA′=a，∴sin∠A′B′O=
=
，∴∠A′B′O=45°，∴∠A′OP'=45°，∴∠POP′=∠A′OP′﹣∠AOP=15°，∴弧PP′的长=
=
πa，即P点运动到P′所经过路线PP′的长为πa．
故答案为：
．
练习册系列答案
阅读快车系列答案
相关题目
