题目内容
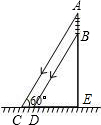 如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.5m,太阳光线与底面的夹角∠ACD=60°,则AB的长为
如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.5m,太阳光线与底面的夹角∠ACD=60°,则AB的长为分析:过D作DE⊥AC于C,过B作BF⊥AC于F.由题意可求得DE=BF=
,再由∠A=30°解直角三角形可求出AB的长度.
| ||
| 2 |
解答: 解:作DE⊥AC于E,BF⊥AC于F.
解:作DE⊥AC于E,BF⊥AC于F.
∵CD=1.5m,∠ACD=60°,
∴DE=BF=
.
在Rt△AFB中∠A=30°,BF=
AB,
∴AB=2BF=
m.
故答案是:
.
 解:作DE⊥AC于E,BF⊥AC于F.
解:作DE⊥AC于E,BF⊥AC于F.∵CD=1.5m,∠ACD=60°,
∴DE=BF=
3
| ||
| 4 |
在Rt△AFB中∠A=30°,BF=
| 1 |
| 2 |
∴AB=2BF=
3
| ||
| 2 |
故答案是:
3
| ||
| 2 |
点评:本题考查解直角三角形的应用,特殊角的三角函数值要熟练掌握.

练习册系列答案
相关题目
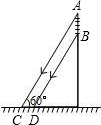 如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1米,太阳光线与地面的夹角∠ACD=60°,则AB的长为( )
如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1米,太阳光线与地面的夹角∠ACD=60°,则AB的长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
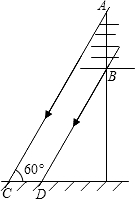 如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2m,太阳光线与地面的夹角∠ACD=60°,则AB的长为
如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1.2m,太阳光线与地面的夹角∠ACD=60°,则AB的长为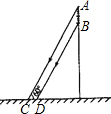 如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1米,太阳光线与地面的夹角∠ACD=60°,则AB的长为
如图,一根电线杆的接线柱部分AB在阳光下的投影CD的长为1米,太阳光线与地面的夹角∠ACD=60°,则AB的长为
 米 B.
米 B.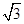 米 C.
米 C.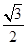 米 D.
米 D. 米
米