题目内容
【题目】如图,已知正方形ABCD的对角线AC、BD交于点O,CE⊥AC与AD边的延长线交于点E.
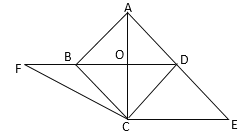
(1)求证:四边形BCED是平行四边形;
(2)延长DB至点F,联结CF,若CF=BD,求∠BCF的大小.
【答案】(1)见解析;(2)∠BCF=15°
【解析】
(1) 利用正方形的性质得出AC⊥DB,BC//AD,再利用平行线的判定与性质结合平行四边形的判定方法得出答案;
(2)利用正方形的性质结合直角三角形的性质得出∠OFC=30°,即可得出答案.
解:(1)证明:∵ABCD是正方形,
∴AC⊥DB,BC∥AD
∵CE⊥AC
∴∠AOD=∠ACE=90°
∴BD∥CE
∴BCED是平行四边形
(2)如图:连接AF,

∵ABCD是正方形,
∴BD⊥AC,BD=AC=2OB=2OC,
即OB=OC
∴∠OCB=45°
∵ Rt△OCF中, CF=BD=2OC,
∴∠OFC=30°
∴∠BCF=60°-45°=15°

练习册系列答案
相关题目