题目内容
 (2011•青浦区一模)如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过A(3,0)、B(1,0)、C(0.3)三点,设该二次函数的顶点为G.
(2011•青浦区一模)如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过A(3,0)、B(1,0)、C(0.3)三点,设该二次函数的顶点为G.(1)求这个二次函数的解析式及其图象的顶点G的坐标;
(2)求tan∠ACG的值;
(3)如该二次函数的图象上有一点P,x轴上有一点E,问是否存在以A、G、E、P为顶点的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)由于A(3,0)、B(1,0)、C(0.3)三点在二次函数y=ax2+bx+c的图象上,直接用待定系数法就可以求出抛物线的解析式,然后化为顶点式就可以求出顶点坐标.
(2)过点G作GH⊥x轴于点H,GF⊥y轴于点F,由勾股定理求出AC、GC、AG从而求得△AGC是直角三角形,从而求得tan∠ACG的值.
(3)当AG为边时,作GH⊥x轴于H,PN⊥x轴于点N,由平行四边形的性质可以得出PE=AG,可以证明PN=GH,可以求出P的坐标,当AG为对角线时,不存在.
(2)过点G作GH⊥x轴于点H,GF⊥y轴于点F,由勾股定理求出AC、GC、AG从而求得△AGC是直角三角形,从而求得tan∠ACG的值.
(3)当AG为边时,作GH⊥x轴于H,PN⊥x轴于点N,由平行四边形的性质可以得出PE=AG,可以证明PN=GH,可以求出P的坐标,当AG为对角线时,不存在.
解答:解:(1)∵A(3,0)、B(1,0)、C(0.3)在二次函数y=ax2+bx+c的图象上,
∴
解得:
,
∴二次函数的解析式为:y=x2-4x+3,
∴y=(x-2)2-1,
∴顶点G(2,-1).
(2)G作GH⊥x轴于点H,GF⊥y轴于点F,
∵G(2,-1)、A(3,0)、B(1,0)、C(0.3),
∴CF=4,GF=2,GH=1,HA=1,在Rt△GFC、Rt△AOC、Rt△GHA中由勾股定理,得
AC2=18,GC2=20,AG2=2
∴△ACG是直角三角形,且∠CAG=90°,
∴tan∠ACG=
=

(3)当AG为边时,作GH⊥x轴于H,PN⊥x轴于点N
∴∠PNE=∠GHA=90°
∵四边形PEGA是平行四边形,
∴PE=AG,∠PEA=∠GAE,
∴△PNE≌△GHA,
∴PN=GH=1,设P(m,1)
∴m2-4m+3=1,
∴m=2±
,
∴P(2±
,1),
当AG为对角线时,不可能.
综上所述,点P的坐标为(2±
,1),

∴
|
解得:
|
∴二次函数的解析式为:y=x2-4x+3,
∴y=(x-2)2-1,
∴顶点G(2,-1).
(2)G作GH⊥x轴于点H,GF⊥y轴于点F,
∵G(2,-1)、A(3,0)、B(1,0)、C(0.3),
∴CF=4,GF=2,GH=1,HA=1,在Rt△GFC、Rt△AOC、Rt△GHA中由勾股定理,得
AC2=18,GC2=20,AG2=2
∴△ACG是直角三角形,且∠CAG=90°,
∴tan∠ACG=
| AG |
| AC |
| 1 |
| 3 |

(3)当AG为边时,作GH⊥x轴于H,PN⊥x轴于点N
∴∠PNE=∠GHA=90°
∵四边形PEGA是平行四边形,
∴PE=AG,∠PEA=∠GAE,
∴△PNE≌△GHA,
∴PN=GH=1,设P(m,1)
∴m2-4m+3=1,
∴m=2±
| 2 |
∴P(2±
| 2 |
当AG为对角线时,不可能.
综上所述,点P的坐标为(2±
| 2 |

点评:本题是一道二次函数的综合试题,考查了待定系数法求抛物线的解析式,勾股定理及勾股定理的逆定理的运用,全等三角形的判定与性质,锐角三角函数的定义.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
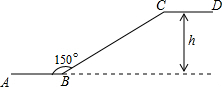 平线,∠ABC=150°,BC的长是a米,则乘电梯从点B到点C上升的高度h是
平线,∠ABC=150°,BC的长是a米,则乘电梯从点B到点C上升的高度h是 (2011•青浦区一模)如图,D是△ABC的边BC上的一点,∠BAD=∠C,∠ABC的平分线分别与AC、AD相交于点E、F,则图形中共有
(2011•青浦区一模)如图,D是△ABC的边BC上的一点,∠BAD=∠C,∠ABC的平分线分别与AC、AD相交于点E、F,则图形中共有