题目内容
花园内有一块边长为a的正方形土地,园艺师设计了四种不同的图案,如下图的A、B、C、D所示,其中的阴影部分用于种植花草.种植花草部分面积最大的图案是( )(说明:A、B、C中圆弧的半径均为
,D中圆弧的半径为a)
| a |
| 2 |
A、 |
B、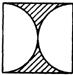 |
C、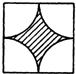 |
D、 |
分析:将第2个图形中的半圆的面积相加为以半径为
的圆;第3个图形中4个扇形的面积相加为以半径为
的圆;故第1,2,3个图形阴影的面积为正方形的面积减去以
为半径的圆的面积;第4个图形的面积为两个扇形的面积减去正方形的面积,计算后比较即可.
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
解答:解:第1,2,3个图形的面积为:a2-π(
)2=(1-
)a2;
第4个图形的面积为:
×2-a2=(
-1)a2;
∵(1-
)a2<(
-1)a2,
∴第4个阴影部分的面积最大.
故选D.
| a |
| 2 |
| π |
| 4 |
第4个图形的面积为:
| 90πa2 |
| 360 |
| π |
| 2 |
∵(1-
| π |
| 4 |
| π |
| 2 |
∴第4个阴影部分的面积最大.
故选D.
点评:解决本题的关键是将每个图形阴影部分面积求出.

练习册系列答案
相关题目

 ,D中圆弧的半径为a)
,D中圆弧的半径为a)



 ,D中圆弧的半径为a)
,D中圆弧的半径为a)



 ,D中圆弧的半径为a)
,D中圆弧的半径为a)


