Question

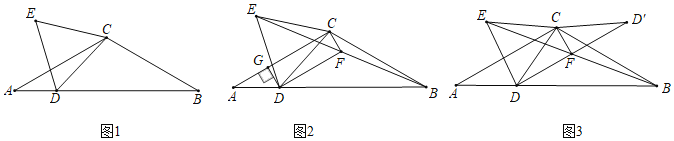
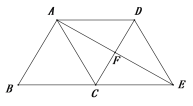
【题目】如图，已知四边形ABCD是平行四边形，AC为一条对角线，且．延长BC到点E，使，连接DE．

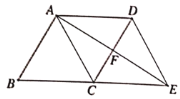
（1）判断四边形ACED的形状，并说明理由；

（2）连接AE交CD于点F，若，，求AE的长．

Answer 1

【答案】（1）菱形，见解析；（2）

【解析】

（1）由已知先证明四边形ACED是平行四边形，再证明AC=AD得出四边形ACED是菱形；

（2） 由四边形ACED是菱形知CE=AC=10，AE=2EF，CD⊥AE，再由得到∠B=60即∠DCE=60，在Rt△CFE中，由勾股定理求出EF，即可求出AE值．

解：(1)四边形ACED是菱形，理由如下：

∵四边形ABCD是平行四边形，

AD∥BC.

∵又CE=AD，

四边形ACED是平行四边形.

∵四边形ABCD是平行四边形，

AB∥CD，

∠BAC=∠ACD，

∵∠BAC=∠ADC，

∠ACD=∠ADC.

AC=AD，

四边形ACED是菱形；

（2）∵ tanB=，

∠B=60°.

∵AB∥BD，

∠DCE=∠B=60°.

∵ 四边形ACED是菱形，

AC=CE=10，AE⊥DC，AE=2EF，

Rt△CFE中，∠DCE=60，

∴∠CEF=30，

∴CF=CE=5，

由勾股定理得EF=.

AE=．