题目内容
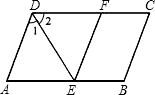 如图所示,DE是?ABCD的∠ADC的平分线,EF∥AD,交DC于F.
如图所示,DE是?ABCD的∠ADC的平分线,EF∥AD,交DC于F.
(1)求证:四边形AEFD是菱形;
(2)如果∠A=60°,AD=5,求菱形AEFD的面积.
(1)证明:∵DF∥AE,EF∥AD,
∴四边形DAEF是平行四边形.
∵∠2=∠AED,∠1=∠2,
∴∠AED=∠1.
∴AD=AE.
∴四边形AEFD是菱形.
(2)解:∵∠A=60°,
∴△AED为等边三角形.
∴DE=5,连接AF与DE相交于O,则EO= .
.
∴OA= =
=
 .
.
∴AF=5 .
.
∴S菱形AEFD= AF•DE=
AF•DE=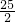
 .
.
分析:(1)可先证明四边形DAEF是平行四边形,再角的关系求得∠AED=∠1,根据等角对等边得AD=AE,再依据有一组邻边相等的平行四边形是菱形可得四边形AEFD是菱形;
(2)由已知求得两条对角线的长,根据菱形的面积等于两条对角线的积的一半,求得菱形的面积.
点评:此题主要考查菱形的性质和判定以及面积的计算,使学生能够灵活运用菱形知识解决有关问题.
∴四边形DAEF是平行四边形.
∵∠2=∠AED,∠1=∠2,
∴∠AED=∠1.
∴AD=AE.
∴四边形AEFD是菱形.
(2)解:∵∠A=60°,

∴△AED为等边三角形.
∴DE=5,连接AF与DE相交于O,则EO=
 .
.∴OA=
 =
=
 .
.∴AF=5
 .
.∴S菱形AEFD=
 AF•DE=
AF•DE=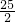
 .
.分析:(1)可先证明四边形DAEF是平行四边形,再角的关系求得∠AED=∠1,根据等角对等边得AD=AE,再依据有一组邻边相等的平行四边形是菱形可得四边形AEFD是菱形;
(2)由已知求得两条对角线的长,根据菱形的面积等于两条对角线的积的一半,求得菱形的面积.
点评:此题主要考查菱形的性质和判定以及面积的计算,使学生能够灵活运用菱形知识解决有关问题.

练习册系列答案
相关题目
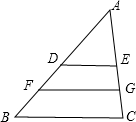 如图所示,DE是△ABC的中位线,FG为梯形BCED的中位线,若BC=8,则FG等于( )
如图所示,DE是△ABC的中位线,FG为梯形BCED的中位线,若BC=8,则FG等于( )| A、2cm | B、3cm | C、4cm | D、6cm |
如图所示,DE是△ABC的中位线,FG是梯形BCED的中位线,若DE=4,即FG等于( )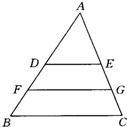

| A、6 | B、8 | C、10 | D、12 |
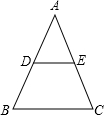 如图所示,DE是△ABC的中位线,BC=8,则DE=
如图所示,DE是△ABC的中位线,BC=8,则DE=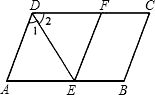 如图所示,DE是?ABCD的∠ADC的平分线,EF∥AD,交DC于F.
如图所示,DE是?ABCD的∠ADC的平分线,EF∥AD,交DC于F.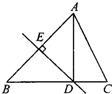 2、如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )
2、如图所示,DE是线段AB的垂直平分线,下列结论一定成立的是( )