Question

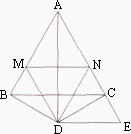
32、如下图是两个等边△ABC、等边△CDE的纸片叠放在一起的图形．

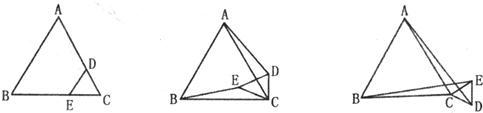
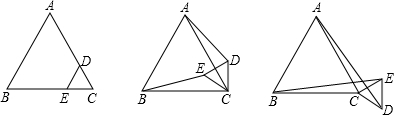
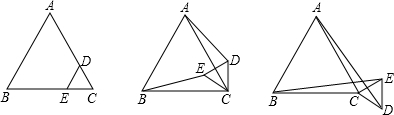
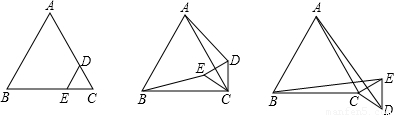
（1）固定△ABC，将△CDE绕点C按顺时针方向旋转30°，连AD，BE，线段BE、AD之间的大小关系如何？证明你的结论；
（2）若将△CDE绕点C按顺时针方向任意旋转一个角度，连AD、BE，线段BE、AD之间大小关系如何，证明你的结论．

Answer 1

分析：（1）根据旋转的性质和等边三角形的性质可以得到∠BCE=∠ACD=30°，CA=CB，CD=CE，由此可证△BCE≌△ACD，然后即可得到BE和AD的关系；
（2）利用和（1）一样的方法证△BCE≌△ACD，由此即可BE和AD的关系．

解答：证明：（1）BE=AD．
∵△CDE绕点C按顺时针方向旋转30°，
∴∠BCE=∠ACD=30°，
又CA=CB，CD=CE，
∴△BCE≌△ACD，
∴BE=AD．

（2）BE=AD，
∵△CDE绕点C按顺时针方向旋转a，
∴∠BCE=∠ACD=a，
又CA=CB，CD=CE，
∴△BCE≌△ACD，
∴BE=AD．

点评：本题主要考查了旋转的性质、全等三角形的判定和性质以及等边三角形的性质．判定两个三角形全等的一般方法有：SSS、SAS、SSA、HL．判定两个三角形全等，先根据已知条件或求证的结论确定那两个三角形可能全等，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．同时利用全等来证明相等的线段是常用的方法之一．