题目内容
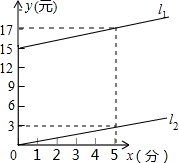
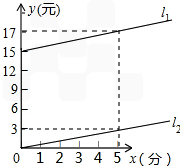
如图,某电信公司关于手机有甲、乙两种收费标准.l1,l2分别表示甲、乙两种收费标 准每月通话费y(元)与通话时间x(分)的函数图象.
准每月通话费y(元)与通话时间x(分)的函数图象.(1)分别求出甲、乙两种收费标准的每月通话费y(元)与通话时间x(分)之间的函数关系式;
(2)若每月通话时间为200分钟,你选择哪类收费方式?
(3)每月通话时间多长时,按甲、乙两类收费标准缴费,所缴话费相等?
分析:(1)用待定系数法求解即可;
(2)把x=200直接代入即可求解;
(3)令
x+15=
x,解之即可;
(2)把x=200直接代入即可求解;
(3)令
| 2 |
| 5 |
| 3 |
| 5 |
解答:解:(1)设y=kx+b
因为l1经过(0,15)和(5,17)两点
所以
,解得
则甲的函数关系式是y=
x+15
因为l2经过(0,0)和(5,3)两点
所以
,解得
则乙的函数关系式是y=
x
(2)把x=200代入y=
x+15中,得y=
×200+15=95(元)
把x=200代入y=
x中,得y=
×200=120(元)
则应选择甲种收费标准.
(3)解
x+15=
x,得x=75
则每月通话75分钟时,收费相同.
因为l1经过(0,15)和(5,17)两点
所以
|
|
则甲的函数关系式是y=
| 2 |
| 5 |
因为l2经过(0,0)和(5,3)两点
所以
|
|
则乙的函数关系式是y=
| 3 |
| 5 |
(2)把x=200代入y=
| 2 |
| 5 |
| 2 |
| 5 |
把x=200代入y=
| 3 |
| 5 |
| 3 |
| 5 |
则应选择甲种收费标准.
(3)解
| 2 |
| 5 |
| 3 |
| 5 |
则每月通话75分钟时,收费相同.
点评:本题意在考查学生利用待定系数法求解一次函数关系式,比较简单.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
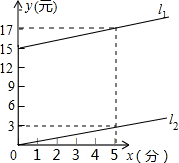 准每月通话费y(元)与通话时间x(分)的函数图象.
准每月通话费y(元)与通话时间x(分)的函数图象.