题目内容
如果a+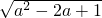 =1成立,那么实数a的范围是
=1成立,那么实数a的范围是
- A.a<1
- B.a≤1
- C.a≥-1
- D.a>-1
B
分析:首先对二次根式进行化简,然后根据题意,推出|a-1|=(1-a),即可推出a-1≤0,解不等式即可.
解答:∵a+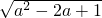 =1,
=1,
∴a+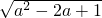 =a+|a-1|=1,
=a+|a-1|=1,
∵a+(1-a)=1,
∴|a-1|=1-a,
∴a-1≤0,
∴a≥1.
故选择B.
点评:本题主要考查二次根式的性质与化简,解不等式,去绝对值号,关键在于掌握非正数的绝对值为其相反数,推出a-1≤0.
分析:首先对二次根式进行化简,然后根据题意,推出|a-1|=(1-a),即可推出a-1≤0,解不等式即可.
解答:∵a+
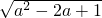 =1,
=1,∴a+
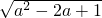 =a+|a-1|=1,
=a+|a-1|=1,∵a+(1-a)=1,
∴|a-1|=1-a,
∴a-1≤0,
∴a≥1.
故选择B.
点评:本题主要考查二次根式的性质与化简,解不等式,去绝对值号,关键在于掌握非正数的绝对值为其相反数,推出a-1≤0.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目

 和
和 同时成立,那需要的条件是
同时成立,那需要的条件是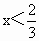 且x¹
-1
且x¹
-1 或x¹
-1
或x¹
-1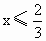 且x¹
-1
且x¹
-1 和
和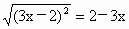 同时成立,那需要的条件是
同时成立,那需要的条件是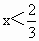 且x¹
-1
且x¹
-1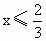 或x¹
-1
或x¹
-1 且x¹
-1
且x¹
-1