题目内容
已知实数a满足|2009-a|+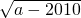 =a,那么a-20092的值是
=a,那么a-20092的值是
- A.2008
- B.2009
- C.2010
- D.2011
C
分析:根据二次根式的被开方数求得m的取值范围,再根据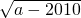 +|2009-a|=a,即可变形得到.
+|2009-a|=a,即可变形得到.
解答:根据题意,得a-2010≥0,即a≥2010;
所以|2009-a|=a-2009,
∵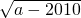 +|2009-a|=a,即
+|2009-a|=a,即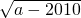 +a-2009=a,
+a-2009=a,
∴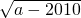 =2009,
=2009,
a-2010=20092,
∴a-20092=2010.
故选C.
点评:本题考查了二次根式的性质,以及二次根式的化简求值,关键是理解得出a的范围后去掉绝对值,技巧性较强.
分析:根据二次根式的被开方数求得m的取值范围,再根据
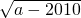 +|2009-a|=a,即可变形得到.
+|2009-a|=a,即可变形得到.解答:根据题意,得a-2010≥0,即a≥2010;
所以|2009-a|=a-2009,
∵
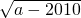 +|2009-a|=a,即
+|2009-a|=a,即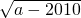 +a-2009=a,
+a-2009=a,∴
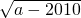 =2009,
=2009,a-2010=20092,
∴a-20092=2010.
故选C.
点评:本题考查了二次根式的性质,以及二次根式的化简求值,关键是理解得出a的范围后去掉绝对值,技巧性较强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
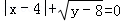 ,则以x,y的值为两边长的等腰三角形的周长是( )
,则以x,y的值为两边长的等腰三角形的周长是( )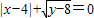 ,则以x,y的值为两边长的等腰三角形的周长是( )
,则以x,y的值为两边长的等腰三角形的周长是( )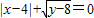 ,则以x,y的值为两边长的等腰三角形的周长是( )
,则以x,y的值为两边长的等腰三角形的周长是( )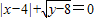 ,则以x,y的值为两边长的等腰三角形的周长是( )
,则以x,y的值为两边长的等腰三角形的周长是( )