题目内容
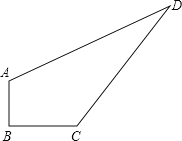
【题目】如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°.
(1)△ACD是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?
【答案】(1)△ACD是直角三角形,∠ACD=90°;(2)3600元.
【解析】试题分析:(1)利用勾股定理可以证明三角形ACD是直角三角形;(2)运用勾股定理可以求得AC的值,同样,可以求出这块草坪的面积,然后就能求得铺满这块空地共需花费的费用.
试题解析:(1)∵∠B=900, AB=3m,BC=4m,
∴AC=![]() =5m,
=5m,
又∵CD=12m,DA=13m,
∴AC2+CD2=DA2,
∴△ACD是直角三角形.
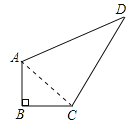
(2)解:连接AC,
则由勾股定理得AC=5m,
∵AC2+DC2=AD2,
∴∠ACD=90°.
这块草坪的面积=SRt△ABC+SRt△ACD=![]() ABBC+
ABBC+![]() ACDC=
ACDC=![]() (3×4+5×12)=36m2.
(3×4+5×12)=36m2.
故需要的费用为36×100=3600元.
答:铺满这块空地共需花费3600元.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目