题目内容
 (2012•乐山)如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An-1BC的平分线与∠An-1CD的平分线交于点An.设∠A=θ.则:
(2012•乐山)如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An-1BC的平分线与∠An-1CD的平分线交于点An.设∠A=θ.则:(1)∠A1=
| θ |
| 2 |
| θ |
| 2 |
(2)∠An=
| θ |
| 2n |
| θ |
| 2n |
分析:(1)根据角平分线的定义可得∠A1BC=
∠ABC,∠A1CD=
∠ACD,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,整理即可得解;
(2)与(1)同理求出∠A2,可以发现后一个角等于前一个角的
,根据此规律即可得解.
| 1 |
| 2 |
| 1 |
| 2 |
(2)与(1)同理求出∠A2,可以发现后一个角等于前一个角的
| 1 |
| 2 |
解答:解:(1)∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,
∴∠A1BC=
∠ABC,∠A1CD=
∠ACD,
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴
(∠A+∠ABC)=
∠ABC+∠A1,
∴∠A1=
∠A,
∵∠A=θ,
∴∠A1=
;
(2)同理可得∠A2=
∠A1=
•
θ=
,
所以∠An=
.
故答案为:(1)
,(2)
.
∴∠A1BC=
| 1 |
| 2 |
| 1 |
| 2 |
又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠A1=
| 1 |
| 2 |
∵∠A=θ,
∴∠A1=
| θ |
| 2 |
(2)同理可得∠A2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| θ |
| 22 |
所以∠An=
| θ |
| 2n |
故答案为:(1)
| θ |
| 2 |
| θ |
| 2n |
点评:本题主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记性质然后推出后一个角是前一个角的一半是解题的关键.

练习册系列答案
相关题目
 (2012•乐山)如图,A、B两点在数轴上表示的数分别为a、b,下列式子成立的是( )
(2012•乐山)如图,A、B两点在数轴上表示的数分别为a、b,下列式子成立的是( ) (2012•乐山)如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:
(2012•乐山)如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论: (2012•乐山)如图,⊙O是四边形ABCD的内切圆,E、F、G、H是切点,点P是优弧
(2012•乐山)如图,⊙O是四边形ABCD的内切圆,E、F、G、H是切点,点P是优弧
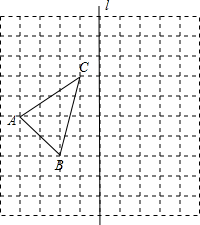 (2012•乐山)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(2012•乐山)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).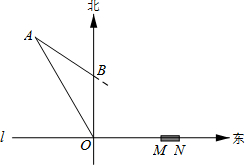 (2012•乐山)如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距
(2012•乐山)如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距