题目内容
【题目】如图,一次函数的图象与反比例函数的图象交于A(﹣3,1)、B(m,3)两点, 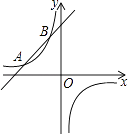
(1)求反比例函数和一次函数的解析式;
(2)写出使一次函数的值大于反比例函数的x的取值范围;
(3)连接AO、BO,求△ABO的面积.
【答案】
(1)解:设一次函数的解析式为y=kx+b(k≠0),反比例函数的解析式为y= ![]() (a≠0),
(a≠0),
把A(﹣3,1)代入y= ![]() 得:a=﹣3,
得:a=﹣3,
即反比例函数的解析式为y=﹣ ![]() ,
,
把B(m,3)代入y=﹣ ![]() 得:3=﹣
得:3=﹣ ![]() ,
,
解得:m=﹣1,
即B的坐标为(﹣1,3),
把A、B的坐标代入y=kx+b得: ![]() ,
,
解得:k=1,b=4,
即一次函数的解析式为y=x+4
(2)解:∵函数y=﹣ ![]() 和y=x+4的交点为A(﹣3,1)、B(﹣1,3),
和y=x+4的交点为A(﹣3,1)、B(﹣1,3),
∴使一次函数的值大于反比例函数的x的取值范围是﹣3<x<﹣1或x>0
(3)解:
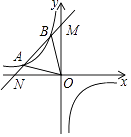
设一次函数y=x+4和x轴的交点为N,和y轴的交点为M,
当x=0时,y=4,当y=0时,x=﹣4,
即OM=4,ON=4,
∵A(﹣3,1)、B(﹣1,3),
∴△ABO的面积为S△MON﹣S△BOM﹣S△AON= ![]() ×4×4﹣
×4×4﹣ ![]() ×4×1﹣
×4×1﹣ ![]() ×4×1=4
×4×1=4
【解析】(1)设一次函数的解析式为y=kx+b(k≠0),反比例函数的解析式为y= ![]() (a≠0),把A(﹣3,1)代入y=
(a≠0),把A(﹣3,1)代入y= ![]() 即可求出反比例函数的解析式,把B(m,3)代入y=﹣
即可求出反比例函数的解析式,把B(m,3)代入y=﹣ ![]() 求出B的坐标,把A、B的坐标代入y=kx+b求出k、b,即可求出一次函数的解析式;(2)根据A、B的坐标和图象得出即可;(3)求出一次函数和两坐标轴的交点坐标,再根据三角形的面积公式求出即可.
求出B的坐标,把A、B的坐标代入y=kx+b求出k、b,即可求出一次函数的解析式;(2)根据A、B的坐标和图象得出即可;(3)求出一次函数和两坐标轴的交点坐标,再根据三角形的面积公式求出即可.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目