题目内容
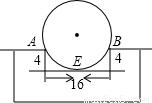
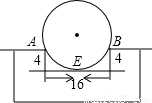
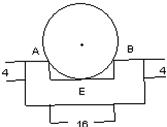 9、如图所示的工件槽的两个底角均为90°,尺寸如图(单位cm),将形状规则的铁球放入槽内,若同时具有A,B,E三个接触点,则该球的半径是( )cm.
9、如图所示的工件槽的两个底角均为90°,尺寸如图(单位cm),将形状规则的铁球放入槽内,若同时具有A,B,E三个接触点,则该球的半径是( )cm.分析:设圆心为O点,连OE,交AB于C,则OE⊥AB,AC=BC=8,在Rt△OAC中,设⊙O的半径为R,OC=R-4,利用勾股定理得到R2=82+(R-4)2,解方程即可.
解答: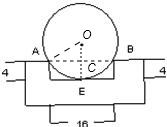
解:设圆心为O点,连OE,交AB于C,如图,
AB=16,CE=4,
则OE⊥AB,
∴AC=BC=8,
在Rt△OAC中,设⊙O的半径为R,OC=R-4,
∴OA2=AC2+OC2,
∴R2=82+(R-4)2,
解得,R=10,
即该球的半径是10cm.
故选A.

解:设圆心为O点,连OE,交AB于C,如图,
AB=16,CE=4,
则OE⊥AB,
∴AC=BC=8,
在Rt△OAC中,设⊙O的半径为R,OC=R-4,
∴OA2=AC2+OC2,
∴R2=82+(R-4)2,
解得,R=10,
即该球的半径是10cm.
故选A.
点评:本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理.

练习册系列答案
相关题目