题目内容
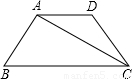
(2009•江西模拟)如图,△ABC中,∠C=90°,AB=6,AC=3,动点P在AB上运动,以点P为圆心,PA为半径画⊙P交AC于点Q.(1)比较AP,AQ的大小,并证明你的结论;
(2)当⊙P与BC相切时,求AP的长,并求此时弓形(阴影部分)的面积.

【答案】分析:(1)Rt△ABC中,根据AB、AC的长,易证得∠A=60°;若连接PQ,则△PAQ是等边三角形,由此可得出AP、AQ的大小关系.
(2)当⊙P与BC相切时,若切点为E,在Rt△PBE中,PB=2PE=2PA,由此可求出⊙P的半径;那么阴影部分的面积可由扇形PAQ和等边△PAQ的面积差求得.
解答: 解:(1)AP=AQ,证明如下:(1分)
解:(1)AP=AQ,证明如下:(1分)
∵∠C=90°,AB=6,AC=3,
∴∠A=60°(2分)
连接PQ,
∴△PQA是等边三角形,即AP=AQ;(3分)
(2)当⊙P与BC相切时,如图,设切点为E,连接PE,则PE⊥BC,(4分)
∴PE∥AC,
∴∠EPB=∠A=60°,
∴PB=2PE=2AP(5分)
即AP=6÷3=2,(6分)
S弧=S扇形PQA-S三角形PQA=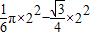 =
= .(8分)
.(8分)
点评:此题主要考查了直角三角形的性质、切线的性质以及扇形的面积公式等.
(2)当⊙P与BC相切时,若切点为E,在Rt△PBE中,PB=2PE=2PA,由此可求出⊙P的半径;那么阴影部分的面积可由扇形PAQ和等边△PAQ的面积差求得.
解答:
 解:(1)AP=AQ,证明如下:(1分)
解:(1)AP=AQ,证明如下:(1分)∵∠C=90°,AB=6,AC=3,
∴∠A=60°(2分)
连接PQ,
∴△PQA是等边三角形,即AP=AQ;(3分)
(2)当⊙P与BC相切时,如图,设切点为E,连接PE,则PE⊥BC,(4分)
∴PE∥AC,
∴∠EPB=∠A=60°,
∴PB=2PE=2AP(5分)
即AP=6÷3=2,(6分)
S弧=S扇形PQA-S三角形PQA=
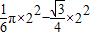 =
= .(8分)
.(8分)点评:此题主要考查了直角三角形的性质、切线的性质以及扇形的面积公式等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(2009•江西模拟)如图,是双胞胎小芳和小菲的照片,有30人看了以后,回答了以下2个问题:
问题①你认为长相中最像的面部部位是哪一个?
调查结果统计如下:
A B C D E B D C C D
B A C C D C C C E A
C C C E A C D B D D
问题②你认为长相中像的面部部位有多少个?调查结果统计如下:
根据以上调查统计结果解答以下问题:
(1)请在如下表格中整理①中的数据,并推断这对双胞胎面部哪个部位最像;
(2)对②中表格统计的数据,我们定义面部长相相像度描述如下,请利用统计量推断这对双胞胎面部相像度是什么.

问题①你认为长相中最像的面部部位是哪一个?
调查结果统计如下:
A B C D E B D C C D
B A C C D C C C E A
C C C E A C D B D D
问题②你认为长相中像的面部部位有多少个?调查结果统计如下:
| 像的部位个数 | 1 | 2 | 3 | 4 | 5 | |
| 回答的人数 | 1 | 3 | 6 | 8 | 10 | 2 |
(1)请在如下表格中整理①中的数据,并推断这对双胞胎面部哪个部位最像;
| A眼睛 | B鼻子 | C嘴巴 | D耳朵 | E脸型 | |
| 划计 | |||||
| 频数 | |||||
| 频率 |
| 面部长相 相像度描述 | 长相一样 | 长相很像 | 长相较像 | 长相相像 | 长相接近 | 长相不像 |
| 面部长相 相像个数x | 5 | 4≤x<5 | 3≤x<4 | 2≤x<3 | 1≤x<2 | x<1 |


 .
.