Question

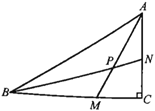
【题目】如图所示，在中，，点在上，且，点在上，且，与相交于点．求证：．

Answer 1

【答案】证明见解析．

【解析】

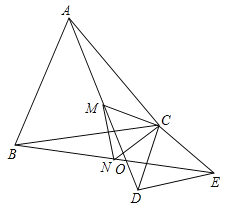
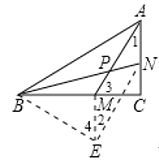
可过点M作ME∥AN，使ME＝AN，连NE，BE，得出四边形AMEN为平行四边形，再通过求证△BEM≌△AMC，可得出△BEN为等腰直角三角形，进而再利用平行线的性质可得出结论．

如图，过M作ME∥AN，使ME＝AN，连NE，BE，

则四边形AMEN为平行四边形，

∴NE＝AM，ME⊥BC，

∵ME＝AN＝CM，∠EMB＝∠MCA＝90 ，BM＝AC，

∴△BEM≌△AMC，得BE＝AM＝NE，∠1＝∠2，∠3＝∠4，

∵∠1＋∠3＝90 ，

∴∠2＋∠4＝90 ，且BE＝NE，

∴△BEN为等腰直角三角形，∠BNE＝45 ，

∵AM∥NE，

∴∠BPM＝∠BNE＝45 ．