题目内容
一个装有进水管和出水管的蓄水池,从某时刻开始的3小时内只进水不出水,在随后的6小时内既进水又出水,每小时进水量和出水量是两个常数,水池内的水 量y(单位:立方米)与时间x(单位:小时)之间的关系如图所示.
量y(单位:立方米)与时间x(单位:小时)之间的关系如图所示.
(1)当0≤x≤3时,写出y与x的函数关系式;
(2)当3≤x≤9时,写出y与x的函数关系式;并求当x=8时,蓄水池中的水有多少?
(3)蓄水池每小时进水、出水各是多少?
解:(1)0≤x≤3时,可设y1=kx+b,当x=0时,y=0,当x=3时,y=12,
得到k=4,b=0,
即y1=4x;
(2)3≤x≤9时,设y2=kx+b,当x=3时,y=12,当x=9时,y=18;
得到k=1,b=9,
即y2=x+9,
所以当x=8时,y=8+9=17,蓄水池中有17立方米的水.
(3)∵y1=4x,
∴每小时进水4立方米,
∵y2=x+9,
∴每小时进水和出水之和为1,则每小时出水3立方米.
分析:(1)从图中可以知道当0≤x≤3时,可设y1=kx+b,当x=0时,y=0,当x=3时,y=12,从而求得当0≤x≤3时,y随x变化的函数关系式;
(2)先求出当3≤x≤9时,y随x变化的函数关系式,即设y2=kx+b,当x=3时,y=12,当x=9时,y=18;从而求出x=8时,蓄水池中的水有多少;
(3)从y1和y2的关系式,y1的变化率可以求出每小时进水,y2的变化率为每小时进水和出水的和.
点评:本题主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题,具备在直角坐标系中的读图能力.
得到k=4,b=0,
即y1=4x;
(2)3≤x≤9时,设y2=kx+b,当x=3时,y=12,当x=9时,y=18;
得到k=1,b=9,
即y2=x+9,
所以当x=8时,y=8+9=17,蓄水池中有17立方米的水.
(3)∵y1=4x,
∴每小时进水4立方米,
∵y2=x+9,
∴每小时进水和出水之和为1,则每小时出水3立方米.
分析:(1)从图中可以知道当0≤x≤3时,可设y1=kx+b,当x=0时,y=0,当x=3时,y=12,从而求得当0≤x≤3时,y随x变化的函数关系式;
(2)先求出当3≤x≤9时,y随x变化的函数关系式,即设y2=kx+b,当x=3时,y=12,当x=9时,y=18;从而求出x=8时,蓄水池中的水有多少;
(3)从y1和y2的关系式,y1的变化率可以求出每小时进水,y2的变化率为每小时进水和出水的和.
点评:本题主要考查用待定系数法求一次函数关系式,并会用一次函数研究实际问题,具备在直角坐标系中的读图能力.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
 20、一个装有进水管和出水管的蓄水池,从某时刻开始的3小时内只进水不出水,在随后的6小时内既进水又出水,每小时进水量和出水量是两个常数,水池内的水量y(单位:立方米)与时间x(单位:小时)之间的关系如图所示.
20、一个装有进水管和出水管的蓄水池,从某时刻开始的3小时内只进水不出水,在随后的6小时内既进水又出水,每小时进水量和出水量是两个常数,水池内的水量y(单位:立方米)与时间x(单位:小时)之间的关系如图所示. 25、一个装有进水管和出水管的蓄水池,从某时刻开始的3小时内只进水不出水,在随后的6小时内既进水又出水,每小时进水量和出水量是两个常数,水池内的水量y(单位:立方米)与时间x(单位:小时)之间的关系如图所示.
25、一个装有进水管和出水管的蓄水池,从某时刻开始的3小时内只进水不出水,在随后的6小时内既进水又出水,每小时进水量和出水量是两个常数,水池内的水量y(单位:立方米)与时间x(单位:小时)之间的关系如图所示. 15、一个装有进水管和出水管的容器,从某一时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进水管.在打开进水管到关停进水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过
15、一个装有进水管和出水管的容器,从某一时刻起只打开进水管进水,经过一段时间,再打开出水管放水,至12分钟时,关停进水管.在打开进水管到关停进水管这段时间内,容器内的水量y(单位:升)与时间x(单位:分钟)之间的函数关系如图所示,关停进水管后,经过 (2013•孝感)如图,一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系.那么,从关闭进水管起
(2013•孝感)如图,一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系.那么,从关闭进水管起 分钟时,容器内的水全部排空.已知此容器每分钟的进水量与出水量均为常数,容器内的水量
分钟时,容器内的水全部排空.已知此容器每分钟的进水量与出水量均为常数,容器内的水量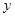 (单位:升)与时间
(单位:升)与时间 (单位:分)之间的函数关系如图所示,请根据图象回答下列问题:
(单位:分)之间的函数关系如图所示,请根据图象回答下列问题:
 时,容器内的水量
时,容器内的水量