题目内容
已知关于x的方程k2x2-(2k-1)x+1=0有两个不相等的实数根,那么使该方程的两个实数根互为相反数的k的值是
- A.不存在
- B.1
- C.-1
- D.

A
分析:首先根据方程有两个不相等的实数根列出有关k的不等式解得k的取值范围,然后根据两个实数根互为相反数求得k的值,看k的值是否使得方程有两个不相等的实数根即可.
解答:∵关于x的方程k2x2-(2k-1)x+1=0有两个不相等的实数根,
∴ ,
,
解得:k< 且k≠0,
且k≠0,
根据一元二次方程根与系数的关系,
有x1+x2= =0,即
=0,即 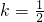 ;
;
但当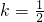 时,△<0,方程无实数根,
时,△<0,方程无实数根,
∴不存在实数k,使方程两根互为相反数.
故选A.
点评:本题考查了一元二次方程根与系数的关系及根的判别式的知识.要掌握根与系数的关系式:x1+x2=- ,x1x2=
,x1x2= .解题时注意二次项系数不为零.
.解题时注意二次项系数不为零.
分析:首先根据方程有两个不相等的实数根列出有关k的不等式解得k的取值范围,然后根据两个实数根互为相反数求得k的值,看k的值是否使得方程有两个不相等的实数根即可.
解答:∵关于x的方程k2x2-(2k-1)x+1=0有两个不相等的实数根,
∴
 ,
,解得:k<
 且k≠0,
且k≠0,根据一元二次方程根与系数的关系,
有x1+x2=
 =0,即
=0,即 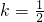 ;
;但当
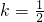 时,△<0,方程无实数根,
时,△<0,方程无实数根,∴不存在实数k,使方程两根互为相反数.
故选A.
点评:本题考查了一元二次方程根与系数的关系及根的判别式的知识.要掌握根与系数的关系式:x1+x2=-
 ,x1x2=
,x1x2= .解题时注意二次项系数不为零.
.解题时注意二次项系数不为零. 
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目