题目内容
如图，两同心圆中，大圆的弦AB的中点为C，已知大圆的半径为5cm，小圆的半径为3cm，弦AB为8cm．（1）AB与小圆有何位置关系？为什么？
（2）圆环的面积是多少？
分析：（1）求出OC的长度，与小圆的半径比较就可以判断位置关系；
（2）圆环的面积=大圆面积-小圆面积．
（2）圆环的面积=大圆面积-小圆面积．
解答：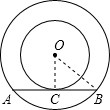
解：（1）相切，
理由：连接OC，OB，则OC⊥AB，
由已知得BC=
AB=4，OB=5，
∴OC=
=
=3，
从而圆心O到直线AB的距离等于小圆的半径，
所以AB与小圆相切；
（2）S环=πOB2-πOC2=π（52-32）=16π（cm）2．
解：（1）相切，理由：连接OC，OB，则OC⊥AB，
由已知得BC=
| 1 |
| 2 |
∴OC=
| OB2+BC2 |
| 52-42 |
从而圆心O到直线AB的距离等于小圆的半径，
所以AB与小圆相切；
（2）S环=πOB2-πOC2=π（52-32）=16π（cm）2．
点评：本题考查：（1）连接半径和弦心距构造直角三角形，利用勾股定理求出弦心距．（2）圆环的面积公式．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
如图，两同心圆中，大圆的弦AB的中点为C，已知大圆的半径为5cm，小圆的半径为3cm，弦AB为8cm．
