题目内容
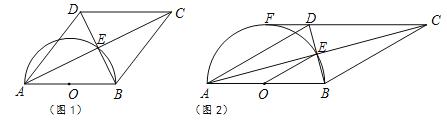
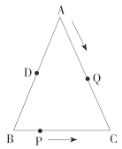
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,如果点
的中点,如果点![]() 在线段
在线段![]() 上以
上以![]() 的速度由点
的速度由点![]() 向点
向点![]() 移动,同时点
移动,同时点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 以
以![]() 的速度移动,若
的速度移动,若![]() 、
、![]() 同时出发,当有一个点移动到点
同时出发,当有一个点移动到点![]() 时,
时,![]() 、
、![]() 都停止运动,设
都停止运动,设![]() 、
、![]() 移动时间为
移动时间为![]() .
.
(1)求![]() 的取值范围.
的取值范围.
(2)当![]() 时,问
时,问![]() 与
与![]() 是否全等,并说明理由.
是否全等,并说明理由.
(3)![]() 时,若
时,若![]() 为等腰三角形,求
为等腰三角形,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 时,
时,![]() 与
与![]() 全等,证明见解析;(3)当
全等,证明见解析;(3)当![]() 或
或![]() 时,
时,![]() 为等腰三角形
为等腰三角形
【解析】
(1)由题意根据图形点的运动问题建立不等式组,进行分析求解即可;
(2)根据题意利用全等三角形的判定定理(SAS),进行分析求证即可;
(3)根据题意分![]() 和
和![]() 以及
以及![]() 三种情况,根据等腰三角形的性质进行分析计算.
三种情况,根据等腰三角形的性质进行分析计算.
(1)依题意![]() ,
,
![]() ,
,
![]() .
.
(2)![]() 时,
时,![]() 与
与![]() 全等,
全等,

证明:![]() 时,
时,![]() ,
,![]() ,在
,在![]() 和
和![]() 中,
中,
∵![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,
![]() ,
,![]() ,
,![]() ,
,
![]() (SAS).
(SAS).
(3)①当![]() 时,有
时,有![]() ;
;
②当![]() ,有
,有![]() ,
,
∵![]() ,
,
∴![]() (舍去);
(舍去);
③当![]() 时有
时有![]() ,
,
∴![]() ;
;
综上,当![]() 或
或![]() 时,
时,![]() 为等腰三角形.
为等腰三角形.

练习册系列答案
相关题目