题目内容
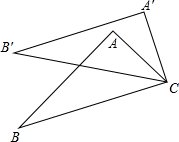 如图,将△ABC绕着C点顺时针旋转到△A'B'C'的位置,若∠BCB′=28°,那么∠ACA′=
如图,将△ABC绕着C点顺时针旋转到△A'B'C'的位置,若∠BCB′=28°,那么∠ACA′=28°
28°
.分析:根据旋转的性质可知△ABC≌△A'B'C',那么∠BCA=∠B′C′A′,即∠1+∠ACB′=∠2+∠ACB′,根据等量相减差相等,可得∠1=∠2,从而易求∠ACA′.
解答: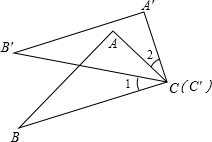 解:如图,
解:如图,
∵△ABC≌△A'B'C',
∴∠BCA=∠B′C′A′,
即∠1+∠ACB′=∠2+∠ACB′,
∴∠1=∠2=28°,
∴∠ACA′=∠2=28°,
故答案是28°.
 解:如图,
解:如图,∵△ABC≌△A'B'C',
∴∠BCA=∠B′C′A′,
即∠1+∠ACB′=∠2+∠ACB′,
∴∠1=∠2=28°,
∴∠ACA′=∠2=28°,
故答案是28°.
点评:本题考查了旋转的性质、全等三角形的判定和性质,解题的关键是知道一个图形旋转后得到的图形和原图形全等.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 4、如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( )
4、如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B′位置,A点落在A′位置,若AC⊥A′B′,则∠BAC的度数是( ) 23、如图,将△ABC绕着顶点A顺时针旋转60°后得到△ADF,这时点F落在BC的中点上.试判断△ABC的形状,并说明理由.
23、如图,将△ABC绕着顶点A顺时针旋转60°后得到△ADF,这时点F落在BC的中点上.试判断△ABC的形状,并说明理由.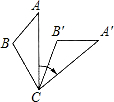 (2012•汕头)如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )
(2012•汕头)如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,则∠BCA′的度数是( )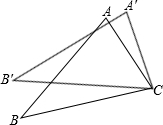 如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B'位置,A点落在A'位置,若AC⊥A'B',则∠BAC的度数是
如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在B'位置,A点落在A'位置,若AC⊥A'B',则∠BAC的度数是