题目内容
【题目】在△ABC中,BD为∠ABC的平分线.
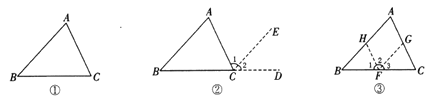
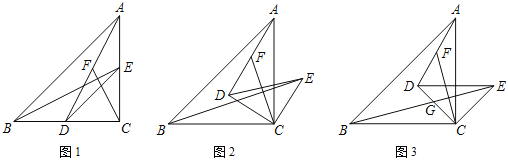
(1)如图1,∠C=2∠DBC,∠A=60°,求证:△ABC为等边三角形;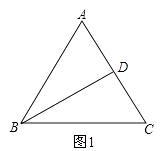
(2)如图2,若∠A=2∠C,BC=8,AB=4.8,求AD的长度;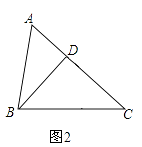
(3)如图3,若∠ABC=2∠ACB,∠ACB的平分线OC与BD相交于点O,且OC=AB,求∠A的度数.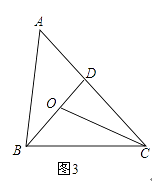
【答案】
(1)
解:∵BD为∠ABC的平分线,
∴∠ABC=2∠DBC
∵∠C=2∠DBC,
∴∠ABC=∠C,
∴AB=AC,
∵∠A=60°,
∴△ABC是等边三角形
(2)
解:如图2,截取BE=AB,连接DE,

在△ABD与△EBD中, 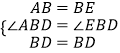 ,
,
∴△ABD≌△EBD,
∴∠A=∠DEB,AD=ED,
∵∠A=2∠C,
∴∠DEB=2∠C,
∵∠DEB=∠C=∠EDB,
∴∠C+∠EDB=2∠C,
∴∠C=∠EDB,
∴ED=EC,
∵AB=4.8,
∴CE=BC﹣BE=3.2,
∴AD=DE=CE=3.2
(3)
解:如图3,过B作BF平分∠DBC交AC于F,

∵BD平分∠ABC,
∴∠ABD=∠CBD= ![]() ∠ABC,
∠ABC,
即∠ABC=2∠ABD=2∠CBD,
∵∠ABC=2∠ACB,
∴∠ACB=∠ABD=∠CBD,
∵OC平分∠ACB,BF平分∠DBC,
∴∠1=∠3= ![]() ∠DBC,∠4=∠2=
∠DBC,∠4=∠2= ![]() ∠ACB,
∠ACB,
∴∠1=∠2=∠3=∠4,
在△OBC与△FCB中,  ,
,
∴△OBC≌△FCB,
∴OC=BF,
∵AB=OC,
∴BF=AB,
∵∠ABF=∠ABD+∠3,∠AFB=∠ACB+∠1,
∵∠ABD=∠ACB,∠1=∠3,
∴∠ABF=∠AFB,
∴AB=AF,
∴AB=BF=AF,
∴△ABF为等边三角形,
∴∠A=60°
【解析】(1)由BD为∠ABC的平分线,得到∠ABC=2∠DBC,等量代换得到∠ABC=∠C,证得AB=AC,即可得到结论;(2)如图2,截取BE=AB,连接DE,推出△ABD≌△EBD,根据全等三角形的性质得到∠A=∠DEB,AD=ED,由∠A=2∠C,得到∠DEB=2∠C,求出∠C=∠EDB,得到ED=EC即可得到结论;(3)过B作BF平分∠DBC交AC于F,根据角平分线的性质得到BD平分∠ABC,∠ABC=2∠ABD=2∠CBD,由∠ABC=2∠ACB,得到∠ACB=∠ABD=∠CBD,由角平分线的定义得到∠1=∠3= ![]() ∠DBC,∠4=∠2=
∠DBC,∠4=∠2= ![]() ∠ACB,推出△OBC≌△FCB,根据全等三角形的性质得到OC=BF,由AB=OC,得到BF=AB等量代换得到∠ABF=∠AFB,求得AB=AF,即可得到结论.
∠ACB,推出△OBC≌△FCB,根据全等三角形的性质得到OC=BF,由AB=OC,得到BF=AB等量代换得到∠ABF=∠AFB,求得AB=AF,即可得到结论.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对角平分线的性质定理的理解,了解定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.

 口算题天天练系列答案
口算题天天练系列答案