题目内容
(2013•宜宾)对于实数a、b,定义一种运算“?”为:a?b=a2+ab-2,有下列命题:
①1?3=2;
②方程x?1=0的根为:x1=-2,x2=1;
③不等式组
的解集为:-1<x<4;
④点(
,
)在函数y=x?(-1)的图象上.
其中正确的是( )
①1?3=2;
②方程x?1=0的根为:x1=-2,x2=1;
③不等式组
|
④点(
| 1 |
| 2 |
| 5 |
| 2 |
其中正确的是( )
分析:根据新定义得到1?3=12+1×3-2=2,则可对①进行判断;根据新定义由x?1=0得到x2+x-2=0,然后解方程可对②进行判断;根据新定义得
,解得-1<x<4,可对③进行判断;
根据新定义得y=x?(-1)=x2-x-2,然后把x=
代入计算得到对应的函数值,则可对④进行判断.
|
根据新定义得y=x?(-1)=x2-x-2,然后把x=
| 1 |
| 2 |
解答:解:1?3=12+1×3-2=2,所以①正确;
∵x?1=0,
∴x2+x-2=0,
∴x1=-2,x2=1,所以②正确;
∵(-2)?x-4=4-2x-2-4=-2x-2,1?x-3=1+x-2-3=x-4,
∴
,解得-1<x<4,所以③正确;
∵y=x?(-1)=x2-x-2,
∴当x=
时,y=
-
-2=-
,所以④错误.
故选C.
∵x?1=0,
∴x2+x-2=0,
∴x1=-2,x2=1,所以②正确;
∵(-2)?x-4=4-2x-2-4=-2x-2,1?x-3=1+x-2-3=x-4,
∴
|
∵y=x?(-1)=x2-x-2,
∴当x=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
故选C.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足二次函数的解析式.也考查了阅读理解能力、解一元二次方程以及解一元一次不等式组.

练习册系列答案
相关题目
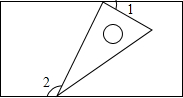 (2013•宜宾)如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2=
(2013•宜宾)如图,一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=25°,则∠2=