题目内容
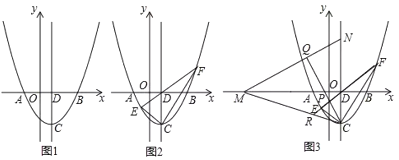
【题目】已知抛物线C1的函数解析式为y=ax2-2x-3a，若抛物线C1经过点(0，-3)．
（1）求抛物线C1的顶点坐标．
（2）已知实数x＞0，请证明x＋
≥2，并说明x为何值时才会有x＋=2；
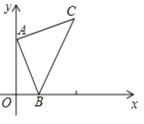
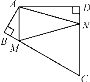
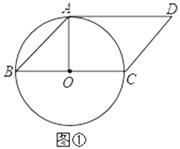
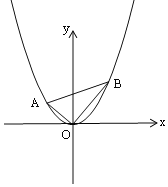
（3）若将抛物线先向上平移4个单位，再向左平移1个单位后得到抛物线C2，设A（m，y1），B（n，y2）是C2上的两个不同点，且满足：∠AOB=90，m＞0，n＜0．请你用含m的表达式表示出△AOB的面积S，并求出S的最小值及S取最小值时一次函数OA的函数解析式．（参考公式：在平面直角坐标系中，若P（x1，y1），Q（x2，y2），则P，Q两点间的距离为
）
【答案】（1）(1，-4)；（2）见解析，当x=1时；（3）1，y=x
【解析】
（1）利用待定系数法求解析式，配方成顶点式后写出顶点坐标即可；
（2）利用平方的非负性可知：
，移项可得结论；
（3）如图所示，根据平移的原则得出
的解析式为：
则
，
，利用勾股定理列式得：
，即
化简得：
，代入面积公式：
，
，从而得出结论．
解：（1）
抛物线过
点，
，
，
，
，
抛物线
的顶点坐标为
；
（2）
，
，
，
显然当
时，才有
；
（3）如图所示，由平移知识易得的解析式为：，
，，
为
△，
，
化简得： ，
，
，
，
的最小值为1，此时
，
，
直线
的一次函数解析式为
．
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案【题目】为了帮助市内一名患“白血病”的中学生，东营市某学校数学社团15名同学积极捐款，捐款情况如下表所示，下列说法正确的是（ ）
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30
【题目】用总长为60米的篱笆围成矩形场地．
（1）根据题意，填写表：
矩形一边长/米 | 5 | 10 | 15 | 20 |
矩形面积/m2 | 125 |
（2）设矩形一边长为x米，矩形面积为S平方米，当x是多少时，矩形场地的面积最大？并求出矩形场地的最大面积；
（3）填空：当矩形的长为 米，宽为 米时，矩形场地的面积为216m2．
