题目内容
当k＜0时，双曲线y=
与直线y=-kx
- A.没有交点
- B.只有一个交点
- C.有两个交点
- D.有三个交点
A
分析：此题可以由k＜0判断函数y=与y=-kx所处的象限，由图象判断函数的交点个数．
解答：k＜0时，函数y=-kx在一、三象限，过原点；
y=在二、四象限且与坐标轴没有交点．
两图象不同在任何一个象限，所以两图象没有交点．
故选A．
点评：本题考查反比例函数与正比例函数的图象特点．
分析：此题可以由k＜0判断函数y=
与y=-kx所处的象限，由图象判断函数的交点个数．解答：k＜0时，函数y=-kx在一、三象限，过原点；
y=
在二、四象限且与坐标轴没有交点．两图象不同在任何一个象限，所以两图象没有交点．
故选A．
点评：本题考查反比例函数与正比例函数的图象特点．
练习册系列答案
相关题目
线部分），对于新的双曲线C2，下列结论：当k＞0时，双曲线y=
与直线y=-kx的公共点有（ ）
| k |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
当k＜0时，双曲线y=
与直线y=-kx（ ）
| k |
| x |
| A、没有交点 |
| B、只有一个交点 |
| C、有两个交点 |
| D、有三个交点 |
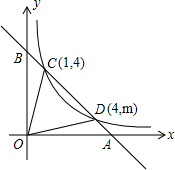如图，一次函数y=ax+b的图象与反比例函数