题目内容
(2006•济宁)随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场.一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:有两种配货方案(整箱配货):| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店______箱,乙店______箱;B种水果甲店______箱,乙店______箱.
(1)如果按照方案一配货,请你计算出经销商能盈利多少元;
(2)请你将方案二填写完整(只写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多;
(3)在甲、乙两店各配货10箱,且保证乙店盈利不少于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
【答案】分析:本题涉及配货方案问题,要根据题意,逐层分析.把每一种的数量和相应的利润对应好,列出一次函数关系式,求自变量取值范围,从而确定一次函数的最大值.
解答:解:(1)按照方案一配货,经销商盈利:
5×11+5×9+5×17+5×13=250(元)
(2)只要求学生填写一种情况.设A种水果给甲x箱,B种水果给甲y箱,则给乙店分别是(10-x)箱,(10-y)箱,根据题意得:11x+17y=9(10-x)+13(10-y),
即2x+3y=22,
则非负整数解是: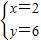 ,
,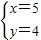 ,
,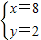 .
.
则第一种情况:2,8,6,4;第二种情况:5,5,4,6;第三种情况:8,2,2,8.
按第一种情况计算:(2×11+17×6)×2=248(元);
按第二种情况计算:(5×11+4×17)×2=246(元);
按第三种情况计算:(8×11+2×17)×2=244(元).
方案一比方案二盈利较多.
(3)设甲店配A种水果x箱,则甲店配B种水果(10-x)箱,
乙店配A种水果(10-x)箱,乙店配B种水果10-(10-x)=x箱.
∵9×(10-x)+13x≥100,
∴x≥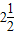
经销商盈利为w=11x+17•(10-x)+9•(10-x)+13x=-2x+260.
∵-2<0,∴w随x增大而减小,
∴当x=3时,w值最大.
方案:甲店配A种水果3箱,B种水果7箱.乙店配A种水果7箱,B种水果3箱.最大盈利:-2×3+260=254(元).
点评:弄清题意,根据题目的不同要求,由易到难解答题目的问题,学会由一次函数表达式及自变量取值范围,求最大值.
解答:解:(1)按照方案一配货,经销商盈利:
5×11+5×9+5×17+5×13=250(元)
(2)只要求学生填写一种情况.设A种水果给甲x箱,B种水果给甲y箱,则给乙店分别是(10-x)箱,(10-y)箱,根据题意得:11x+17y=9(10-x)+13(10-y),
即2x+3y=22,
则非负整数解是:
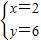 ,
,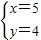 ,
,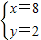 .
.则第一种情况:2,8,6,4;第二种情况:5,5,4,6;第三种情况:8,2,2,8.
按第一种情况计算:(2×11+17×6)×2=248(元);
按第二种情况计算:(5×11+4×17)×2=246(元);
按第三种情况计算:(8×11+2×17)×2=244(元).
方案一比方案二盈利较多.
(3)设甲店配A种水果x箱,则甲店配B种水果(10-x)箱,
乙店配A种水果(10-x)箱,乙店配B种水果10-(10-x)=x箱.
∵9×(10-x)+13x≥100,
∴x≥
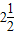
经销商盈利为w=11x+17•(10-x)+9•(10-x)+13x=-2x+260.
∵-2<0,∴w随x增大而减小,
∴当x=3时,w值最大.
方案:甲店配A种水果3箱,B种水果7箱.乙店配A种水果7箱,B种水果3箱.最大盈利:-2×3+260=254(元).
点评:弄清题意,根据题目的不同要求,由易到难解答题目的问题,学会由一次函数表达式及自变量取值范围,求最大值.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
(2006•济宁)随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场.一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:有两种配货方案(整箱配货):
方案一:甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱;
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店______箱,乙店______箱;B种水果甲店______箱,乙店______箱.
(1)如果按照方案一配货,请你计算出经销商能盈利多少元;
(2)请你将方案二填写完整(只写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多;
(3)在甲、乙两店各配货10箱,且保证乙店盈利不少于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店______箱,乙店______箱;B种水果甲店______箱,乙店______箱.
(1)如果按照方案一配货,请你计算出经销商能盈利多少元;
(2)请你将方案二填写完整(只写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多;
(3)在甲、乙两店各配货10箱,且保证乙店盈利不少于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
(2006•济宁)随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场.一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:有两种配货方案(整箱配货):
方案一:甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱;
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店______箱,乙店______箱;B种水果甲店______箱,乙店______箱.
(1)如果按照方案一配货,请你计算出经销商能盈利多少元;
(2)请你将方案二填写完整(只写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多;
(3)在甲、乙两店各配货10箱,且保证乙店盈利不少于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店______箱,乙店______箱;B种水果甲店______箱,乙店______箱.
(1)如果按照方案一配货,请你计算出经销商能盈利多少元;
(2)请你将方案二填写完整(只写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多;
(3)在甲、乙两店各配货10箱,且保证乙店盈利不少于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
(2006•济宁)随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场.一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:有两种配货方案(整箱配货):
方案一:甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱;
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店______箱,乙店______箱;B种水果甲店______箱,乙店______箱.
(1)如果按照方案一配货,请你计算出经销商能盈利多少元;
(2)请你将方案二填写完整(只写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多;
(3)在甲、乙两店各配货10箱,且保证乙店盈利不少于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店______箱,乙店______箱;B种水果甲店______箱,乙店______箱.
(1)如果按照方案一配货,请你计算出经销商能盈利多少元;
(2)请你将方案二填写完整(只写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多;
(3)在甲、乙两店各配货10箱,且保证乙店盈利不少于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
(2006•济宁)随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场.一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售,预计每箱水果的盈利情况如下表:有两种配货方案(整箱配货):
方案一:甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱;
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店______箱,乙店______箱;B种水果甲店______箱,乙店______箱.
(1)如果按照方案一配货,请你计算出经销商能盈利多少元;
(2)请你将方案二填写完整(只写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多;
(3)在甲、乙两店各配货10箱,且保证乙店盈利不少于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店______箱,乙店______箱;B种水果甲店______箱,乙店______箱.
(1)如果按照方案一配货,请你计算出经销商能盈利多少元;
(2)请你将方案二填写完整(只写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多;
(3)在甲、乙两店各配货10箱,且保证乙店盈利不少于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?