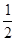题目内容
若方程x2=m的解是有理数,则实数m不能取下列四个数中的( )A.1
B.4
C.

D.

【答案】分析:将原方程直接开平方求得x=±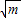 ,然后根据条件方程x2=m的解是有理数,利用排除法解答此题.
,然后根据条件方程x2=m的解是有理数,利用排除法解答此题.
解答:解:解方程x2=m,得
x=±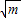 ;
;
∵方程x2=m的解是有理数,
∴m是完全平方数;
A、∵(±1)2=1,∴1符号要求;故本选项错误;
B、∵(±2)2=4,∴4符号要求;故本选项错误;
C、∵(± )2=
)2= ,∴
,∴ 符号要求;故本选项错误;
符号要求;故本选项错误;
D、∵(±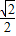 )2=
)2= ,而
,而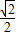 是无理数;故本选项正确;
是无理数;故本选项正确;
故选D.
点评:本题考查了解一元二次方程--直接开平方法.用直接开方法求一元二次方程的解的类型有:x2=a(a≥0);ax2=b(a,b同号且a≠0);(x+a)2=b(b≥0);a(x+b)2=c(a,c同号且a≠0).法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”.
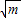 ,然后根据条件方程x2=m的解是有理数,利用排除法解答此题.
,然后根据条件方程x2=m的解是有理数,利用排除法解答此题.解答:解:解方程x2=m,得
x=±
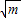 ;
;∵方程x2=m的解是有理数,
∴m是完全平方数;
A、∵(±1)2=1,∴1符号要求;故本选项错误;
B、∵(±2)2=4,∴4符号要求;故本选项错误;
C、∵(±
 )2=
)2= ,∴
,∴ 符号要求;故本选项错误;
符号要求;故本选项错误;D、∵(±
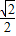 )2=
)2= ,而
,而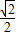 是无理数;故本选项正确;
是无理数;故本选项正确;故选D.
点评:本题考查了解一元二次方程--直接开平方法.用直接开方法求一元二次方程的解的类型有:x2=a(a≥0);ax2=b(a,b同号且a≠0);(x+a)2=b(b≥0);a(x+b)2=c(a,c同号且a≠0).法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
若方程x2=m的解是有理数,则实数m不能取下列四个数中的( )
| A、1 | ||
| B、4 | ||
C、
| ||
D、
|
若方程x2=m的解是有理数,则实数m不能取下列四个数中的( )
| A.1 | B.4 | C. | D.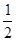 |
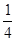 D.
D.