题目内容
【题目】如图①,在平面直角坐标系中,平行于x轴的直线与抛物线y=ax(a>0)相交于A、B两点.设点B的横坐标为m(m>0).
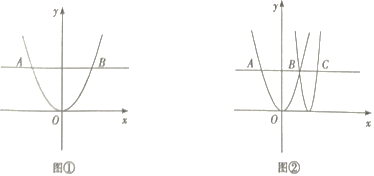
(1)求AB的长(用含m的代数式表示).
(2)如图②,点C在直线AB上,点C的横坐标为2m.若a=1,m=2,求顶点在x轴上且经过B、C两点的抛物线的顶点坐标.
(3)点D在直线AB上,BD=2AB,过O、B、D三点的抛物线的顶点为P,其对应函数的二次项系数为a1.
①求![]() 的值.
的值.
②当m=2,△BPD为等腰直角三角形,直接写出a的值.
【答案】(1)AB的长为2m;
(2)抛物线的顶点坐标为(3,0).
(3)①![]() 的值是
的值是![]() ;②a的值为
;②a的值为![]() 或
或![]() .
.
【解析】试题分析:(1)根据A、B两点关于y轴对称,可得A点的横坐标,然后求解即可;
(2)把a和m的值代入,然后根据顶点式直接可求解;
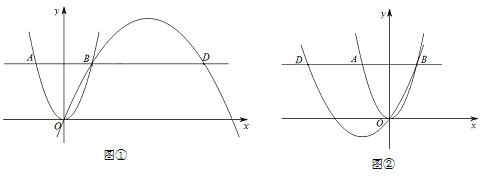
(3)①如图①,点D在点B右侧,设过O、B、D三点的抛物线解析式,然后通过待定系数法可求解;如图②,点D在点B左侧,设过O、B、D三点的抛物线所对应函数表达式同样可求解;②代入求值即可.
试题解析:(1)∵点B的横坐标为m,点A与点B关于y轴对称,
∴点A的横坐标为-m.
AB=m-(- m)=2m.
(2)把x=2代入y=x,得y=4.∴点B的坐标为(2,4).
∵2m=4,∴点C的坐标为(4,4).
∵BC∥x轴,∴点B、C关于这条抛物线的对称轴对称.
∴该对称轴为直线x=3.
∵顶点在x轴上,∴这个顶点坐标为(3,0).
另解:
∵m=2,∴ xB=2,xC=4.
∵BC∥x轴,∴点B、C关于这条抛物线的对称轴对称.
∴该对称轴为直线x=3.
∵顶点在x轴上,∴这个顶点坐标为(3,0)
(3)①如图①,点D在点B右侧,设过O、B、D三点的抛物线所对应函数表达式为![]() ,把(0,0)代入得,
,把(0,0)代入得, ![]() .
.
∴![]() .
.
∵点B的坐标为(m,am),
∴![]() ,∴
,∴![]() .
.
如图②,点D在点B左侧,设过O、B、D三点的抛物线所对应函数表达式为
![]() ,把(0,0)代入得,
,把(0,0)代入得, ![]() .
.
∴![]() .
.
∵点B的坐标为![]() ,
,
∴![]() ,∴
,∴![]() .
.
②![]() 或
或![]() .
.

【题目】下表记录了某种幼树在一定条件下移植成活情况
移植总数n | 400 | 1500 | 3500 | 7000 | 9000 | 14000 |
成活数m | 325 | 1336 | 3203 | 6335 | 8073 | 12628 |
成活的频率(精确到0.01) | 0.813 | 0.891 | 0.915 | 0.905 | 0.897 | 0.902 |
由此估计这种幼树在此条件下移植成活的概率约是_____(精确到0.1).