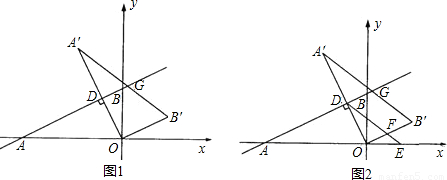题目内容
(2008•哈尔滨)如图,在平面直角坐标系中,直线y=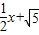 与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.
与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.(1)求点D的坐标;
(2)连接DE,当DE与线段OB′相交,交点为F,且四边形DFB′G是平行四边形时,(如图2)求此时线段DE所在的直线的解析式;
(3)若以动点为E圆心,以
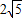 为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′=
为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′= ?并判断此时直线A′O与⊙E的位置关系,请说明理由.
?并判断此时直线A′O与⊙E的位置关系,请说明理由.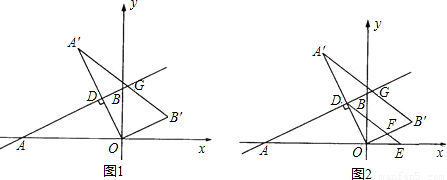
【答案】分析:现根据直线y=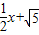 与x轴、y轴分别交于A、B两点,求出A、B两点的坐标,进而再求出OD的长度;然后根据需要作出恰当的辅助线,再结合题意对题目进行分析.
与x轴、y轴分别交于A、B两点,求出A、B两点的坐标,进而再求出OD的长度;然后根据需要作出恰当的辅助线,再结合题意对题目进行分析.
解答: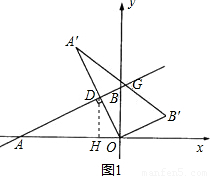 解:(1)由题意知A(
解:(1)由题意知A(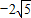 ,0)B(0,
,0)B(0, ),
),
∴OA= ,OB=
,OB=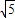 ,
,
∴AB=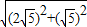 =5,
=5,
∵OD⊥AB,
∴ OA•OB=
OA•OB= AB•OD,
AB•OD,
∴OD= =2.
=2.
过点D作DH⊥x轴于点H.(如图1)
∵∠BAO+∠ADH=∠ODH+∠ADH=90°,
∴∠ODH=∠BAO,
∴tan∠ODH=tan∠BAO= ,
,
∴DH=2OH.
设OH=a,则DH=2a.
∴a2+4a2=4,
∴a=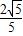 .
.
∴OH=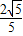 ,DH=
,DH=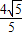 .
.
∴D(-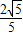 ,
,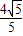 );
);
(2)设DE与y轴交于点M.(如图2)
∵四边形DFB′G是平行四边形,
∴DF∥B′G,
∴∠1=∠A′.
又∵∠AOD+∠2=∠AOD+∠OAD=90°,
∴∠BAO=∠2.
∵∠BAO=∠A′,
∴∠1=∠2,
∴DM=OM.(1分)
∵∠3+∠1=90°,∠4+∠2=90°,
∴∠3=∠4,
∴BM=DM,
∴BM=OM,
∴点M是OB中点,
∴M(0,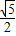 ).
).
设线段DE所在直线解析式为y=kx+b.
把M(0, )D(
)D(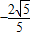 ,
,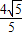 )代入y=kx+b,
)代入y=kx+b,
得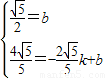 ,解得
,解得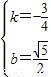 .
.
∴线段DE所在直线的解析式为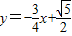 ;
;
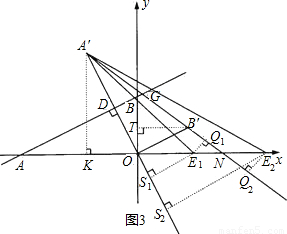
(3)设直线A′B′交x轴于点N,(如图3)过点A′作A′K⊥x轴于点K.
∵∠AOD=∠A′OK,∠ADO=∠A′KO=90°,OA=OA′=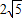 ,
,
∴△AOD≌△A′OK,
∴OK=2,
∴A′K=4,
∴A′(-2,4).
过点B′作B′T⊥y轴于点T,同理△OBD≌△B′OT,
∴B′(2,1).
设直线A’B’的解析式为y=k1x+b1.
则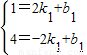 ,解得
,解得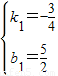 .
.
∴直线A′B′的解析式为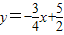 .
.
∴N(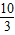 ,0),
,0),
∴KN=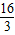 ,
,
∴A’N=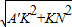 =
=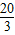 .
.
当E点在N点左侧点E1位置时,过点E1作E1Q1⊥A’N于点Q1.
∵tan∠A’NK=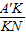 =
= ,
,
∴设E1Q1=3m,则Q1N=4m.
又∵tan∠E1A’B’= ,
,
∴A’Q1=24m,
∴28m=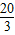 ,
,
∴m=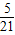 ,
,
∴E1N=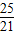 ,
,
∴OE1=ON-E1N=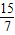 ,此时t=
,此时t=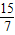 .
.
过点E1作E1S1⊥A’O于点S1.
∵sin∠E1OS1=sin∠A′OK,
∴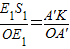 ,
,
∴E1S1= .
.
∵⊙E的半径为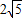 ,而
,而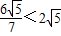 ,
,
∴⊙E1与直线A’O相交.
当E点在N点右侧点E2位置时,
过点E2作E2Q2⊥A′N于点Q2.
同理OE2=5,此时t=5.
过点E2作E2S2⊥A′O于点S2.
同理E2S2=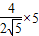 =
=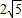 .
.
∵⊙E的半径为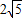 ,
,
∴⊙E2与直线A′O相切.
∴当t=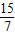 或t=5时,tan∠EA′B′=
或t=5时,tan∠EA′B′= ;
;
当t= 时直线A′O与⊙E相交,当t=5时直线A′O与⊙E相切.
时直线A′O与⊙E相交,当t=5时直线A′O与⊙E相切.
点评:解决较复杂的几何问题,作出合适的辅助线是解决问题的一个关键,同时要熟记一些定理或推论.
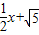 与x轴、y轴分别交于A、B两点,求出A、B两点的坐标,进而再求出OD的长度;然后根据需要作出恰当的辅助线,再结合题意对题目进行分析.
与x轴、y轴分别交于A、B两点,求出A、B两点的坐标,进而再求出OD的长度;然后根据需要作出恰当的辅助线,再结合题意对题目进行分析.解答:
 解:(1)由题意知A(
解:(1)由题意知A(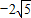 ,0)B(0,
,0)B(0, ),
),∴OA=
 ,OB=
,OB=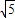 ,
,∴AB=
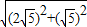 =5,
=5,∵OD⊥AB,
∴
 OA•OB=
OA•OB= AB•OD,
AB•OD,∴OD=
 =2.
=2.过点D作DH⊥x轴于点H.(如图1)
∵∠BAO+∠ADH=∠ODH+∠ADH=90°,
∴∠ODH=∠BAO,
∴tan∠ODH=tan∠BAO=
 ,
,∴DH=2OH.
设OH=a,则DH=2a.
∴a2+4a2=4,
∴a=
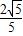 .
.∴OH=
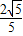 ,DH=
,DH=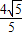 .
.∴D(-
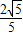 ,
,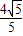 );
);(2)设DE与y轴交于点M.(如图2)
∵四边形DFB′G是平行四边形,
∴DF∥B′G,
∴∠1=∠A′.
又∵∠AOD+∠2=∠AOD+∠OAD=90°,
∴∠BAO=∠2.
∵∠BAO=∠A′,
∴∠1=∠2,
∴DM=OM.(1分)

∵∠3+∠1=90°,∠4+∠2=90°,
∴∠3=∠4,
∴BM=DM,
∴BM=OM,
∴点M是OB中点,
∴M(0,
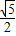 ).
).设线段DE所在直线解析式为y=kx+b.
把M(0,
 )D(
)D(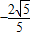 ,
,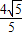 )代入y=kx+b,
)代入y=kx+b,得
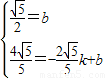 ,解得
,解得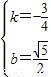 .
.∴线段DE所在直线的解析式为
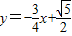 ;
;(3)设直线A′B′交x轴于点N,(如图3)过点A′作A′K⊥x轴于点K.
∵∠AOD=∠A′OK,∠ADO=∠A′KO=90°,OA=OA′=
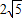 ,
,∴△AOD≌△A′OK,
∴OK=2,
∴A′K=4,
∴A′(-2,4).
过点B′作B′T⊥y轴于点T,同理△OBD≌△B′OT,
∴B′(2,1).
设直线A’B’的解析式为y=k1x+b1.
则
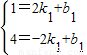 ,解得
,解得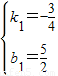 .
.∴直线A′B′的解析式为
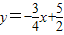 .
.∴N(
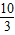 ,0),
,0),∴KN=
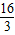 ,
,∴A’N=
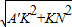 =
=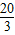 .
.当E点在N点左侧点E1位置时,过点E1作E1Q1⊥A’N于点Q1.
∵tan∠A’NK=
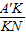 =
= ,
,∴设E1Q1=3m,则Q1N=4m.
又∵tan∠E1A’B’=
 ,
,∴A’Q1=24m,
∴28m=
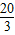 ,
,∴m=
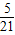 ,
,∴E1N=
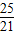 ,
,∴OE1=ON-E1N=
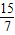 ,此时t=
,此时t=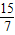 .
.过点E1作E1S1⊥A’O于点S1.
∵sin∠E1OS1=sin∠A′OK,
∴
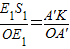 ,
,∴E1S1=
 .
.
∵⊙E的半径为
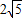 ,而
,而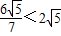 ,
,∴⊙E1与直线A’O相交.
当E点在N点右侧点E2位置时,
过点E2作E2Q2⊥A′N于点Q2.
同理OE2=5,此时t=5.
过点E2作E2S2⊥A′O于点S2.
同理E2S2=
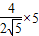 =
=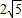 .
.∵⊙E的半径为
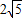 ,
,∴⊙E2与直线A′O相切.
∴当t=
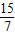 或t=5时,tan∠EA′B′=
或t=5时,tan∠EA′B′= ;
;当t=
 时直线A′O与⊙E相交,当t=5时直线A′O与⊙E相切.
时直线A′O与⊙E相交,当t=5时直线A′O与⊙E相切.点评:解决较复杂的几何问题,作出合适的辅助线是解决问题的一个关键,同时要熟记一些定理或推论.

练习册系列答案
相关题目
 与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.
与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.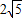 为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′=
为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′= ?并判断此时直线A′O与⊙E的位置关系,请说明理由.
?并判断此时直线A′O与⊙E的位置关系,请说明理由.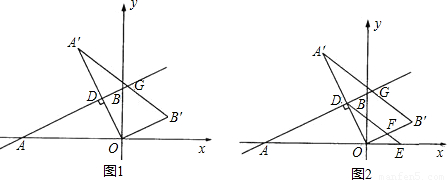
 与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.
与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒. 为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′=
为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′= ?并判断此时直线A′O与⊙E的位置关系,请说明理由.
?并判断此时直线A′O与⊙E的位置关系,请说明理由.
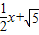 与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.
与x轴、y轴分别交于A、B两点,将△ABO绕原点O顺时针旋转得到△A′B′O,并使OA′⊥AB,垂足为D,直线AB与线段A´B´相交于点G.动点E从原点O出发,以1个单位/秒的速度沿x轴正方向运动,设动点E运动的时间为t秒.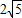 为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′=
为半径作⊙E,连接A′E,t为何值时,Tan∠EA′B′= ?并判断此时直线A′O与⊙E的位置关系,请说明理由.
?并判断此时直线A′O与⊙E的位置关系,请说明理由.