题目内容
如图,A、B两点的坐标分别为(4,0),(0,3),动点P从O点出发沿x轴正方向以每秒2个单位的速度运动,动点Q从B点出发以每秒一个单位的速度向O点运动,点P、Q分别从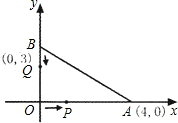 O、B同时出发,当Q运动到原点O时,点P随之停止运动,设运动时间为t(秒).
O、B同时出发,当Q运动到原点O时,点P随之停止运动,设运动时间为t(秒).
(1)设△POQ的面积为s,求s与t的函数关系式;
(2)当线段PQ与AB相交于点E,且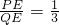 时,求∠QPO的正切值;
时,求∠QPO的正切值;
(3)当t为何值时,以O、P、Q为顶点的三角形与△ABO相似.
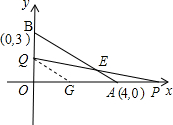 解:(1)∵OP=2t,BQ=t,
解:(1)∵OP=2t,BQ=t,∴OQ=3-t,
∴S=
 •2t(3-t)=t(3-t)(0≤t≤3);
•2t(3-t)=t(3-t)(0≤t≤3);(2)如图所示:作QG∥AB,
∴
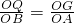 ,
,∴
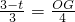 ,
,∴OG=4-
 t,
t,∵
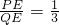 ,
,∴
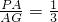 ,
,∴
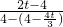 =
= ,
,∴t=
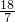 ,
,∴tan∠QPO=
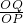 =
= ;
;(3)∵∠AOB=∠POQ,
∴当
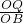 =
=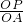 或
或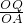 =
=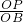 时,两三角形相似,即
时,两三角形相似,即∴
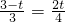 或
或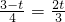 ,
,∴t=
 或t=
或t= ,
,∴当t=
 或t=
或t= 时,以O、P、Q为顶点的三角形与△ABO相似.
时,以O、P、Q为顶点的三角形与△ABO相似.分析:(1)根据题意,用t表示OP,OQ的长,用三角形的面积公式表示s,结合图形写出t的范围;
(2)根据已知比例,构造平行线,作QG∥AB,利用平行线分线段成比例定理求OG,再用比例代换的方法求t,在直角△OPQ中求∠QPO的正切值;
(3)由于∠AOB=∠POQ,那么两个三角形相似,有两种对应关系:△PQO∽△ABO,△QPO∽△ABO,按照对应边的比相等,分别求解.
点评:本题考查了面积的求法,利用平行构造相似比、相似三角形及其比例,根据题意寻找相似三角形的条件,本题还运用了分类讨论的思想,具有较强的综合性.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
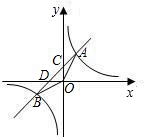 如图,一次函数y=kx+b的图象经过第一、二、三象限,且与反比例函数图象相交于A,B两点,与y轴交于点C,与x轴交于点D,OB=
如图,一次函数y=kx+b的图象经过第一、二、三象限,且与反比例函数图象相交于A,B两点,与y轴交于点C,与x轴交于点D,OB= 8、如图,从城市A到城市B有三种不同的交通工具:汽车、火车、飞机,除去速度因素,坐飞机的时间最短是因为
8、如图,从城市A到城市B有三种不同的交通工具:汽车、火车、飞机,除去速度因素,坐飞机的时间最短是因为 20、当你去看电影的时候,你想坐得离屏幕近一些,可是又不想为了看屏幕边缘的镜头不停地转动眼睛.如图所示,点A、B分别为屏幕边缘两点,若你在P点,则视角为∠APB.如果你觉得电影院内P点是观看的最佳位置,可是已经有人坐在那了,那么你会找到一个位置Q,使得在Q、P两点有相同的视角吗?请在图中画出来(保留画图痕迹,不写画法).
20、当你去看电影的时候,你想坐得离屏幕近一些,可是又不想为了看屏幕边缘的镜头不停地转动眼睛.如图所示,点A、B分别为屏幕边缘两点,若你在P点,则视角为∠APB.如果你觉得电影院内P点是观看的最佳位置,可是已经有人坐在那了,那么你会找到一个位置Q,使得在Q、P两点有相同的视角吗?请在图中画出来(保留画图痕迹,不写画法). (2013•河北一模)如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是
(2013•河北一模)如图,已知直线y=x+4与两坐???轴分别交于A、B两点,⊙C的圆心坐标为 (2,O),半径为2,若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值和最大值分别是