题目内容
△ABC中∠A=40°,点P在△ABC外,且BP平分∠B,CP平分∠C的外角,则∠P的度数为( )
| A、20° | B、40° | C、50° | D、70° |
分析:首先画出图形,设∠C的外角为∠ACD,在△ABC、△CPB中,根据三角形的外角性质可得:∠ACD=∠A+∠ABC,∠DCP=∠CBP+∠P,联立两式可求得∠P的度数.
解答: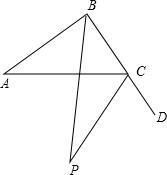 解:依题意,可得右图:
解:依题意,可得右图:
△ABC中,外角∠ACD=∠A+∠ABC,
即
∠ACD=
∠A+
∠ABC?
∠ACD=
∠ABC+20°①;
△CPB中,外角∠CDP=∠CBP+∠P,
由题意知:∠CBP=
∠ABC,∠DCP=
∠ACD,
即
∠ACD=
∠ABC+∠P②;
联立①②,得:∠P=20°.
故选A.
 解:依题意,可得右图:
解:依题意,可得右图:△ABC中,外角∠ACD=∠A+∠ABC,
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
△CPB中,外角∠CDP=∠CBP+∠P,
由题意知:∠CBP=
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
联立①②,得:∠P=20°.
故选A.
点评:此题主要考查的是三角形的外角性质以及角平分线的定义.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
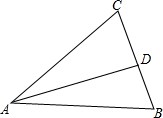 如图,在△ABC中∠BAC=40°,∠B=75°,AD是△ABC的角平分线,求∠ADB的度数.
如图,在△ABC中∠BAC=40°,∠B=75°,AD是△ABC的角平分线,求∠ADB的度数. 如图,△ABC中∠A=40°,AB=AC,D为△ABC内的一点,且∠DCA=∠DBC,则∠BDC=( )
如图,△ABC中∠A=40°,AB=AC,D为△ABC内的一点,且∠DCA=∠DBC,则∠BDC=( )