题目内容
观察本题的三个图形,思考下列问题
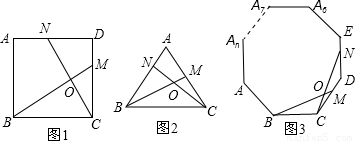
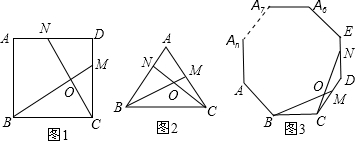
(1)如图1,正方形ABCD中,点M是CD上异于端点的任意一点,过点C作CN⊥BM于O,且交AD于N点.求证:BM=CN;
(2)如图2,等边△ABC中,点M是CA上异于端点的任意一点,过点C作射线CN交AB于点N、交BM于点O,且使∠BOC=120°.
请你判断此时BM与CN的大小关系,并证明你的结论.
(3)如图3,正n边形ABCDE…An中,点M是CD上异于端点的任意一点,过点C作射线CN交DE于点N、交BM于点O,且使BM=CN.设此时∠BOC的大小为y,请你写出y与n之间的函数关系式.
解:(1)∵正方形ABCD,CN⊥BM,
∴CD=BC,∠MBC=∠NCD,
∴△BCM≌△CDN,
∴BM=CN;
(2)∵等边△ABC,
∴AC=BC,∠A=∠ACB=60°,
∵∠BOC=120°,
∴∠ACN=∠CBM,
∴△BCM≌△CAN,
∴BM=CN;
(3)∵正n边形ABCDE…An中,
∴∠BCM=∠CDN,
∵BM=CN,BC=CD,
∴△BCM≌△CDN,
∴∠OCD=∠CBO,
∴∠BOC=180°-∠CBO-∠BCO=180°-∠BCD,
∴∠BOC=180°-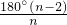 ,
,
∴y= .
.
分析:(1)根据题意,推出△BCM≌△CDN,即可;
(2)BM=CN,根据题意推出∠A=∠BCM=60°,∠ACN=∠CBM,可得△BCM≌△CAN,即可推出结论;
(3)根据题意推出△BCM≌△CDN,即得∠OCD=∠CBO,由∠BOC=180°-∠CBO-∠BCO=180°-∠BCD,即可推出y= .
.
点评:本题主要考查全等三角形的判定和性质、等边三角形的性质、正多边形的性质、关键在于求证相关三角形全等.
∴CD=BC,∠MBC=∠NCD,
∴△BCM≌△CDN,
∴BM=CN;
(2)∵等边△ABC,
∴AC=BC,∠A=∠ACB=60°,
∵∠BOC=120°,
∴∠ACN=∠CBM,
∴△BCM≌△CAN,
∴BM=CN;
(3)∵正n边形ABCDE…An中,
∴∠BCM=∠CDN,
∵BM=CN,BC=CD,
∴△BCM≌△CDN,
∴∠OCD=∠CBO,
∴∠BOC=180°-∠CBO-∠BCO=180°-∠BCD,
∴∠BOC=180°-
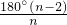 ,
,∴y=
 .
.分析:(1)根据题意,推出△BCM≌△CDN,即可;
(2)BM=CN,根据题意推出∠A=∠BCM=60°,∠ACN=∠CBM,可得△BCM≌△CAN,即可推出结论;
(3)根据题意推出△BCM≌△CDN,即得∠OCD=∠CBO,由∠BOC=180°-∠CBO-∠BCO=180°-∠BCD,即可推出y=
 .
.点评:本题主要考查全等三角形的判定和性质、等边三角形的性质、正多边形的性质、关键在于求证相关三角形全等.

练习册系列答案
相关题目