题目内容
【题目】(9分)已知:如图,在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点
的图象交于点![]() 和点和
和点和![]() .
.
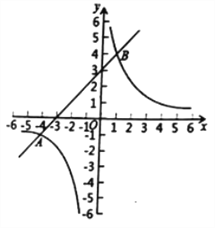
(1)求这两个函数的表达式;
(2)观察图象,当![]() 时,直接写出自变量
时,直接写出自变量![]() 的取值范围;
的取值范围;
(3)求![]() 的面积.
的面积.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】试题分析:(1)利用待定系数法求得反比例函数解析式,把B的坐标代入反比例函数解析式求得B的坐标,然后利用待定系数求得一次函数解析式;
(2)利用函数图象,求![]() 时自变量
时自变量![]() 的取值范围,就是求反比例函数图象在上边时对应的
的取值范围,就是求反比例函数图象在上边时对应的![]() 的范围;
的范围;
(3)求得![]() 与
与![]() 轴的交点,然后利用三角形的面积公式求解.
轴的交点,然后利用三角形的面积公式求解.
试题解析:(1)∵函数![]() 的图象过点
的图象过点![]() ,
,
∴![]() ,
,
∴反比例函数解析式为: ![]() ,
,
又∵点![]() 在
在![]() 上,
上,
∴![]() ,∴
,∴![]()
又∵一次函数![]() 过
过![]() ,
, ![]() 两点,
两点,
∴![]() ,
,
解得![]() .
.
∴一次函数解析式为: ![]() .
.
(2)若![]() ,则函数
,则函数![]() 的图象总在函数
的图象总在函数![]() 的图象上方,
的图象上方,
∴![]() 或
或![]() .
.
(3)连接![]() 交
交![]() 轴于
轴于![]() ,
,
则点![]() ,
, ![]() ,
,
![]() 的面积
的面积![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元