题目内容
 如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④
如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④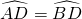 .其中一定成立的是
.其中一定成立的是
- A.①②③
- B.②③④
- C.①③④
- D.①②④
D
分析:①易证△CDE≌△CDF,得CE=CF;②∠ACB+∠ACE=180°,根据四边形内角和定理得∠ACE+∠EDF=180°,所以∠ACB=∠EDF;③没理由证明DE是切线;④根据圆内接四边形的外角等于内对角得∠DCE=∠DAB,所以∠DAB=∠DCA,根据圆周角定理判断弧AD=弧BD.
解答: 解:①∵∠DCE=∠DCF,∠DEC=∠DFC,DC=DC,
解:①∵∠DCE=∠DCF,∠DEC=∠DFC,DC=DC,
∴△CDE≌△CDF,得CE=CF.故成立;
②∠ACB+∠ACE=180°,根据四边形内角和定理得∠ACE+∠EDF=180°,所以∠ACB=∠EDF,故成立;
③连接OD、OC.则∠ODC=∠OCD.假如DE是切线,则OD⊥DE,因BE⊥DE,所以OD∥BE,∠DCE=∠ODC=∠OCD,而∠DCE=∠DCA,∠OCD≠∠DCA,故DE不是切线;
④根据圆内接四边形的外角等于内对角得∠DCE=∠DAB,所以∠DAB=∠DCA,根据圆周角定理判断弧AD=弧BD.故成立.
故选D.
点评:此题考查的知识点较多,综合性较强,有一定难度.
分析:①易证△CDE≌△CDF,得CE=CF;②∠ACB+∠ACE=180°,根据四边形内角和定理得∠ACE+∠EDF=180°,所以∠ACB=∠EDF;③没理由证明DE是切线;④根据圆内接四边形的外角等于内对角得∠DCE=∠DAB,所以∠DAB=∠DCA,根据圆周角定理判断弧AD=弧BD.
解答:
 解:①∵∠DCE=∠DCF,∠DEC=∠DFC,DC=DC,
解:①∵∠DCE=∠DCF,∠DEC=∠DFC,DC=DC,∴△CDE≌△CDF,得CE=CF.故成立;
②∠ACB+∠ACE=180°,根据四边形内角和定理得∠ACE+∠EDF=180°,所以∠ACB=∠EDF,故成立;
③连接OD、OC.则∠ODC=∠OCD.假如DE是切线,则OD⊥DE,因BE⊥DE,所以OD∥BE,∠DCE=∠ODC=∠OCD,而∠DCE=∠DCA,∠OCD≠∠DCA,故DE不是切线;
④根据圆内接四边形的外角等于内对角得∠DCE=∠DAB,所以∠DAB=∠DCA,根据圆周角定理判断弧AD=弧BD.故成立.
故选D.
点评:此题考查的知识点较多,综合性较强,有一定难度.

练习册系列答案
相关题目
 如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④
如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④ |
| AD |
 |
| BD |
| A、①②③ | B、②③④ |
| C、①③④ | D、①②④ |
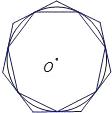 如图,⊙O的内接多边形周长为3,⊙O的外切多边形周长为3.4,则下列各数中与此圆的周长最接近的是( )
如图,⊙O的内接多边形周长为3,⊙O的外切多边形周长为3.4,则下列各数中与此圆的周长最接近的是( )A、
| ||
B、
| ||
C、
| ||
D、
|
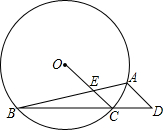 OC交AB于E.
OC交AB于E. 如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=
如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB= 如图,⊙O的内接四边形ABCD中,AB=AD,∠BAD=30°,AC=4,求四边形ABCD的面积.
如图,⊙O的内接四边形ABCD中,AB=AD,∠BAD=30°,AC=4,求四边形ABCD的面积.