Question

作图、说理和计算：如图，已知△ABC，
（1）完成下列作图：
①用尺规作AC边上的中线BD（保留痕迹，不写作法）；
②画AB边上的高CE，
（2）把△ABD绕点D旋转180°，画出经变换后的像△CDF，连接AF，线段AF与线段BC相等吗？说明理由．
（3）在上述（1），（2）所画图形中，已知CE=4，S_△ADF=10，求S_△ABC及AB的长．

Answer 1

分析：（1）①作出AC的垂直平分线交AC于点D，连接BD即为所求的线段；
②以点C为圆心，较大的长为半径画弧，交直线BA于两点，分别以这两点为圆心，大于这两点的距离的一半为半径画弧，两弧相交于一点，过点C及这点画直线，交AB的延长线于一点E，CE就是所求的线段；
（2）延长BD到F，可得△CDF，易证△ADF≌△BCD，那么AF=BC；
（3）△ABC的面积为△ADF的面积的2倍，根据三角形的面积公式可得AB的长．

解答：解：（1）①如图，线段BD即为所求的AC边上的中线；
②如图，线段CE即为所求的AB边上的高，

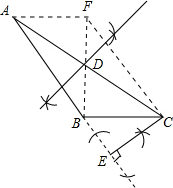
（2）线段AF与线段BC相等，理由如下：
AD=CD，
在△ADF与△BCD中，∠ADF=∠CDB，
DF=BD
∴△ADF≌△BCD，
∴AF=BC；

（3）∵△ADF≌△CBD，
∴S_△BCD=S_△ADF=10，
∵AD=DC，
∴S_△ABC=2S_△BCD=20，
∴

1

2

×AB×CE=20，
∵CE=4，
∴AB=10．

点评：三角形全等，那么面积相等；等底同高的三角形的面积相等；三角形的一边上的高等于三角形的面积的2倍除以这边的长．