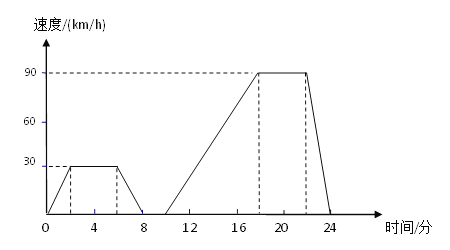
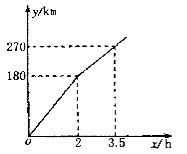
题目内容
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M.
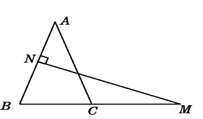
(1)若∠A=40°,求∠NMB的度数.
(2)如果将(1)中∠A的度数改为70°,其余条件不变,求∠NMB的度数.
(3)由(1)(2)你发现了什么规律?并说明理由.
【答案】(1) 20°;(2) 35°;
(3)规律:∠NMB=![]() ∠A.
∠A.
【解析】(1)根据等边对等角,由AB=AC可得到∠ABM=∠ACB,再结合已知∠A的度数,即可求出∠NMB的度数;
(2)仿照第(1)问的求解过程即可得到∠NMB的度数;
(3)结合上述两问的解答,即可发现∠NMB和∠A之间的大小关系,然后仿照上述解答过程进行验证即可.
解:(1)∵AB=AC,
∴∠ABM=∠ACB.
∵∠BAC=40°,∠ABM=∠ACB,
∴∠ABM=![]() ×(180°-∠BAC)=70°.
×(180°-∠BAC)=70°.
∵MN是AB的垂直平分线,∠ABM=70°,
∴∠NMB=90°-∠ABM=90°-70°=20°.
(2)与(1)同理可得∠B=![]() ×(180°-∠BAC)=55°,
×(180°-∠BAC)=55°,
∴∠NMB=90°-55°=35°.
(3)规律:在等腰△ABC中,当AB=AC,∠NMB的度数恰好为顶角∠A度数的一半,即∠NMB=![]() ∠A.理由如下:
∠A.理由如下:
∵AB=AC,
∴∠ABM=∠ACB.
∴∠ABM=![]() (180°-∠A)=90°-
(180°-∠A)=90°-![]() ∠A.
∠A.
∵∠ABM=90°-![]() ∠A,∠BNM=90°,
∠A,∠BNM=90°,
∴∠BMN=90°-∠ABM=![]() ∠A.
∠A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目