Question

【题目】已知，在平面直角坐标系中，AB⊥x轴于点B，点A（a，b）满足 +|b﹣2|=0，平移线段AB使点A与原点重合，点B的对应点为点C．
（1）则a= ， b=；点C坐标为；
（2）如图1，点D（m，n）在线段BC上，求m、n满足的关系式；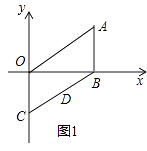

（3）如图2，E是线段OB上一动点，以OB为边作∠BOG=∠AOB，交BC于点G，连CE交OG于点F，当点E在线段OB上运动过程中， 的值是否会发生变化？若变化请说明理由，若不变，请求出其值．

Answer 1

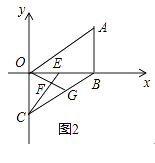
【答案】
（1）4；2；（0，﹣2）
（2）

解：如图1，过点D分别作DM⊥x轴于点M，DN⊥y轴于点N，连接OD．

∵AB⊥x轴于点B，且点A，D，C三点的坐标分别为：（4，2），（m，n），（0，﹣2），

∴OB=4，OC=2，MD=﹣n，ND=m，

∴S△BOC= OB×OC=4，

又∵S△BOC=S△BOD+S△COD

= OB×MD+ OC×ND

= ×4×（﹣n）+ ×m×2

=m﹣2n，

∴m、n满足的关系式为：m﹣2n=4

（3）

解： 的值不变，值为2．

理由如下：

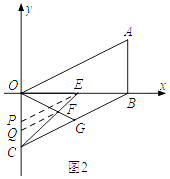
如图2，分别过点E，F作EP∥OA，FQ∥OA分别交y轴于点P，点Q，

∵线段OC是由线段AB平移得到，

∴BC∥OA，

又∵EP∥OA，

∴EP∥BC，

∴∠GCF=∠PEC，

∵EP∥OA，

∴∠AOE=∠OEP，

∴∠OEC=∠OEP+∠PEC=∠AOE+∠GCF，①

同理：∠OFC=∠AOF+∠GCF，

又∵∠AOB=∠BOG，

∴∠OFC=2∠AOE+∠GCF，②

根据①，②可得：

= =2．

【解析】解：（1）∵ +|b﹣2|=0，
∴a﹣4=0，b﹣2=0，
∴a=4，b=2，
∵AB=OC=2，且C在y轴负半轴上，
∴C（0，﹣2），
所以答案是：4，2，（0，﹣2）；
【考点精析】本题主要考查了平行线的性质的相关知识点，需要掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补才能正确解答此题．