��Ŀ����
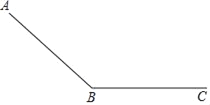
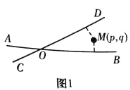
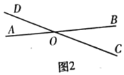
����Ŀ�����壺��ͼ1��ƽ��������ֱ��AB��CD�ཻ�ڵ�O������ƽ��������һ��M����M��ֱ��AB��CD�ľ���ֱ�Ϊp��q���������ʵ����(p��q)�ǵ�M�ġ��������ꡱ�������������壬���������ꡱΪ��0��0���ĵ���1��������O��
��1�����������ꡱΪ1��0�ĵ��� ����
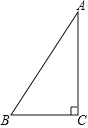
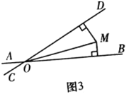
��2����ͼ2������M�ڹ���O����ֱ��AB��ֱ��ֱ��l��ʱ����M�ġ��������ꡱΪp��q����BOD 150����д��p��q�Ĺ�ϵʽ��֤����
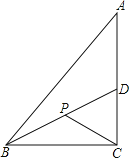
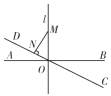
��3����ͼ3����M�ġ��������ꡱΪ![]() ����DOB 30����OM�ij���
����DOB 30����OM�ij���
���𰸡�(1)2��(2)![]() ��(3)
��(3)![]()
��������
��1�������������������Ķ�����ͼ���жϼ��ɣ�
��2����M��MN��CD��N��������֪�ó�![]() ��
��![]() �������MON��60�������ݺ�30��ֱ�������ε����ʺ��ɶ������
�������MON��60�������ݺ�30��ֱ�������ε����ʺ��ɶ������![]() ���ɽ�����⣻
���ɽ�����⣻
��3���ֱ�����![]() ����
����![]() ��
��![]() �ĶԳƵ�
�ĶԳƵ�![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() �ֱ�
�ֱ�![]() ��
��![]() ��
��![]() �㡢
�㡢![]() �㣬����֤��
�㣬����֤��![]() �����
�����![]() ��
��![]() ��Ȼ���
��Ȼ���![]() ��
��![]() ����
����![]() �ӳ�����
�ӳ�����![]() �����ݺ�30��ֱ�������ε��������
�����ݺ�30��ֱ�������ε��������![]() ��
��![]() �������ù��ɶ������EF���ɣ�
�������ù��ɶ������EF���ɣ�
�⣺��1���������֪����ֱ��CD�ϣ����ڵ�O���������һ������2����
�ʴ�Ϊ��2��
��2����![]() ��
��![]() ��
��![]() ��
��
��ֱ��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
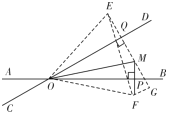
��3���ֱ�����![]() ����
����![]() ��
��![]() �ĶԳƵ�
�ĶԳƵ�![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ������
������![]() ��
��![]() �ֱ�
�ֱ�![]() ��
��![]() ��
��![]() �㡢
�㡢![]() �㣮
�㣮
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
����OEF�ǵȱ������Σ�
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ����
����![]() �ӳ�����
�ӳ�����![]() ��
��
��![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��


����Ŀ��ij��˾10������Ա��ȥ����ɵ����۶���������
���۶��λ����Ԫ�� | 3 | 4 | 5 | 6 | 7 | 8 | 10 |
����Ա��������λ���ˣ� | 1 | 3 | 2 | 1 | 1 | 1 | 1 |
��1�������۶��ƽ��������������λ����
��2�����깫˾Ϊ�˵���Ա�������ԣ���������۶����ȡ�����н��Ĵ�ʩ������ݣ�1���Ľ����ͨ���Ƚϣ�����ȷ������ÿ������Աͳһ�����۶���Ƕ�����Ԫ��
����Ŀ����ͼ��һ�������ɻ��£�AB�Σ��ͻ������BC�Σ���ɣ���ѩ���ڻ����ϻ��еľ���y1����λ��m���ͻ���ʱ��t1����λs��������κ�����ϵ�������������ݣ�
����ʱ��t1/s | 0 | 1 | 2 | 3 | 4 |
�����y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
��ѩ���ڻ�����ϻ��еľ���y2����λ��m���ͻ���ʱ��t2����λ��s�����㣺y2=52t2��2t22����ѩ�ߴ�A�����ڻ����BC��ֹͣ��һ������23s��
��1����y1��t1����Ķ��κ�������ʽ��
��2������AB�ij��ȣ�