题目内容
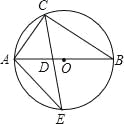
【题目】如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。AF平分∠CAB,交CD于点E,交CB于点F。
(1)求证:CE=CF。
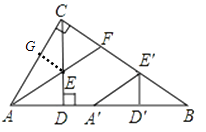
(2)将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图(2)所示。试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
【答案】
(1)证明:∵AF平分∠CAB,∴∠CAF=∠EAD,∵∠ACB=90°,∴∠CAF+∠CFA=90°,∵CD⊥AB,∴∠EAD+∠AED=90°, ∴∠CFA=∠AED ,又∵∠AED=∠CEF,∴∠CFA=∠AED,∴CE=CF
(2)答: ![]() =CF. 过点E作EG⊥AC于点G,
=CF. 过点E作EG⊥AC于点G,
∵AF平分∠CAB,ED⊥AB,EG⊥AC,
∴ED=EG,
∵△ADE平移得到 ![]() ,
,
∴ ![]() =DE,
=DE,
∴ ![]() =GE,
=GE,
∵∠ACB=90°,
∴∠ACD+∠DCB=90°,
∵CD⊥AB,
∴∠B+∠DCB=90°,
∴∠ACD=∠B,在△CEG和 ![]() 中,
中,
∵ 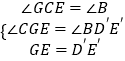 ,∴△CEG≌
,∴△CEG≌ ![]() (AAS),∴CE=
(AAS),∴CE= ![]() ,又∵CE=CF,∴
,又∵CE=CF,∴ ![]() =CF
=CF
【解析】(1)求证CE=CF可由等角对等边,即若∠CFA=∠AED,则CE=CF。由AF平分∠CAB,∠CAF=∠EAD再利用互余关系易得结果。
(2)过点E作EG⊥AC于点G,由角平分线的性质可得ED=EG,再由平移可得 D ′ E ′ =GE,还有互余关系可得∠ACD=∠B,以及两个直角,最后得证△CEG≌ △ B E ′ D ′推得 B E ′ =CF。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目