题目内容
A地产汽油,B地需要汽油,汽车自A地运汽油往B地,往返所需的汽油正好等于满载汽油的吨数,故无法直接自A地运往B地.因此,需在中途设一油库为中间站C,自A往返于A、C间的汽车将油从A地运送至C地,然后再由往返于C、B间的汽车将油从C地运至B地.设A、B两地的路程为s,B地收到的汽油吨数与A地运出汽油的吨数之比为运油率k.
(1)当AC= s时,求运油率k的值.
s时,求运油率k的值.
(2)当AC为何值时,运油率最大?并求出此时的运油率k.
解:(1)设满车载油a吨,则汽车从A地灌油到C地,可输入油库 a吨,
a吨,
故A地到C地的运油率为 ,
,
同理:C地到B地的运油率为 ,
,
∴k= ×
× =
=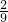 ;
;
(2)设AC=x,则A地到C地的运油率为1-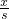 ,
,
C地到B地的运油率为1-(1-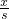 )=
)=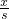 ,
,
∴A地到B地的运油率k=(1-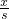 )•
)•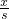 =-
=-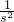 x2+
x2+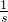 x,
x,
∴当x=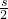 时,运油率k最大为
时,运油率k最大为 .
.
分析:(1)首先设满车载油a吨,根据题意,由AC= s,即可得汽车从A地灌油到C地,可输入油库
s,即可得汽车从A地灌油到C地,可输入油库 a吨,则可求得A地到C地的运油率,继而求得C地到B地的运油率,求其积即是运油率k的值.
a吨,则可求得A地到C地的运油率,继而求得C地到B地的运油率,求其积即是运油率k的值.
(2)与(1)类似,首先设AC=x,则可求得A地到C地的运油率为1-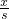 ,继而求得C地到B地的运油率,根据二次函数最值的求解方法,即可求得答案.
,继而求得C地到B地的运油率,根据二次函数最值的求解方法,即可求得答案.
点评:此题考查了二次函数的实际应用问题.此题难度较大,解题的关键是理解题意,能根据题意求得A地到C地的运油率与C地到B地的运油率,得到二次函数,根据二次函数性质的求解.
 a吨,
a吨,故A地到C地的运油率为
 ,
,同理:C地到B地的运油率为
 ,
,∴k=
 ×
× =
=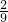 ;
;(2)设AC=x,则A地到C地的运油率为1-
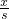 ,
,C地到B地的运油率为1-(1-
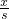 )=
)=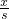 ,
,∴A地到B地的运油率k=(1-
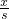 )•
)•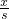 =-
=-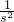 x2+
x2+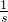 x,
x,∴当x=
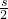 时,运油率k最大为
时,运油率k最大为 .
.分析:(1)首先设满车载油a吨,根据题意,由AC=
 s,即可得汽车从A地灌油到C地,可输入油库
s,即可得汽车从A地灌油到C地,可输入油库 a吨,则可求得A地到C地的运油率,继而求得C地到B地的运油率,求其积即是运油率k的值.
a吨,则可求得A地到C地的运油率,继而求得C地到B地的运油率,求其积即是运油率k的值.(2)与(1)类似,首先设AC=x,则可求得A地到C地的运油率为1-
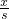 ,继而求得C地到B地的运油率,根据二次函数最值的求解方法,即可求得答案.
,继而求得C地到B地的运油率,根据二次函数最值的求解方法,即可求得答案.点评:此题考查了二次函数的实际应用问题.此题难度较大,解题的关键是理解题意,能根据题意求得A地到C地的运油率与C地到B地的运油率,得到二次函数,根据二次函数性质的求解.

练习册系列答案
相关题目
 s时,求运油率k的值.
s时,求运油率k的值.